【题目】已知电流在一定时间段内正常通过电子元件的概率是0.5,用列表或画树状图的方法分别求在一定时间段内,A、B之间和C、D之间电流能够正常通过的概率.(提示:可用1、0分别表示电子元件的通与不通两种状态) 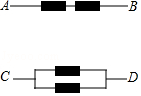
参考答案:
【答案】解:(1)根据题意画树状图: 
由图可得,共有4种情况,其中A、B之间的两个元件都通过电流的有一种,故所求的概率P= ![]() ;
;
⑵根据题意画树状图:
由图可得,总共有4种情况,其中C、D之间两个元件中至少有一个元件通电的情况有3种,故所求的概率P= ![]()
【解析】由题意可知,AB段若有一个元件断开,那AB段就断开;而CD段只有一个元件通电,那CD段通电,画出树状图求解即可.
【考点精析】认真审题,首先需要了解列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,解答后面的问题.
解方程:
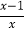 -
-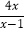 =0.
=0.解:设y=
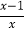 ,则原方程可化为y-
,则原方程可化为y-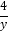 =0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.
=0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.经检验,y1=2,y2=-2都是方程y-
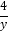 =0的解.
=0的解.当y=2时,
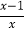 =2,解得x=-1;当y=-2时,
=2,解得x=-1;当y=-2时,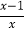 =-2,解得x=
=-2,解得x= .
.经检验,x1=-1,x2=
 都是原分式方程的解.所以原分式方程的解为x1=-1,x2=
都是原分式方程的解.所以原分式方程的解为x1=-1,x2= .
.上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程
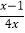 -
-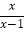 =0中,设y=
=0中,设y=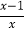 ,则原方程可化为________________;
,则原方程可化为________________;(2)若在方程
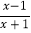 -
-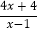 =0中,设y=
=0中,设y=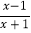 ,则原方程可化为________________;
,则原方程可化为________________;(3)模仿上述换元法解方程:
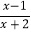 -
-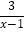 -1=0.
-1=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,
, ,点D、E为BC边上的两点,且
,点D、E为BC边上的两点,且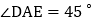 ,连接EF、BF则下列结论:
,连接EF、BF则下列结论: ≌
≌ ;
;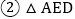 ≌
≌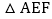 ;
; ;
; ,其中正确的有()个.
,其中正确的有()个.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在平面直角坐标系中,对
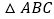 进行循环往复的轴对称变换,若原来点A坐标是
进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2019次变换后所得的A点坐标是________.
,则经过第2019次变换后所得的A点坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
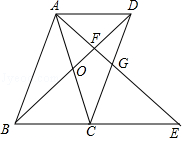
(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°
(1)求∠GFC的度数:
(2)求证:DM∥BC.

相关试题

