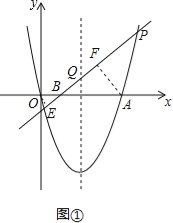
【题目】如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.

(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ;
(2)若两个三角形面积满足S△POQ=![]() S△PAQ,求m的值;
S△PAQ,求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD![]() DQ的最大值.
DQ的最大值.
参考答案:
【答案】(1)x=2,45;(2)m=-1或2;(3)①6![]() ;②18.
;②18.
【解析】试题分析:(1)把解析式转化成顶点式,或利用对称轴公式即可得该抛物线的对称轴,利用直线y=x+m与坐标轴的交点坐标即可求得直线PQ与x轴所夹锐角的度数;(2)分情况讨论,即直线PQ与x轴的交点落在OA的延长线上,OA上,AO的延长线上三种情况讨论m值.设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,,当点B在OA的延长线时,S△POQ=![]() S△PAQ不成立;当点B落在线段OA上时,
S△PAQ不成立;当点B落在线段OA上时, ![]() ,由△OBE∽△ABF得,
,由△OBE∽△ABF得, ![]() ,由对称轴求出A点坐标,再由比例式求出B点坐标,代入直线PQ解析式,即可求得m值;当点B落在线段AO的延长线上时,同理由比例式求出B点坐标,进而确定m值;(3)①由题意可过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,AD⊥PH,DQ=DH,PD+DQ=PH,过P点作PM⊥CH于点M,可得△PMH是等腰直角三角形,PH=
,由对称轴求出A点坐标,再由比例式求出B点坐标,代入直线PQ解析式,即可求得m值;当点B落在线段AO的延长线上时,同理由比例式求出B点坐标,进而确定m值;(3)①由题意可过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,AD⊥PH,DQ=DH,PD+DQ=PH,过P点作PM⊥CH于点M,可得△PMH是等腰直角三角形,PH=![]() PM,即当PM最大时,PH最大,显然当点P在抛物线顶点处时,PM最大,此时PM=6,于是求得PH的最大值.即PD+DQ的最大值;②上题求得PD+DQ的最大值为6
PM,即当PM最大时,PH最大,显然当点P在抛物线顶点处时,PM最大,此时PM=6,于是求得PH的最大值.即PD+DQ的最大值;②上题求得PD+DQ的最大值为6![]() .即PD+DQ ≤6
.即PD+DQ ≤6![]() ,设PD=a,则DQ ≤6
,设PD=a,则DQ ≤6![]() -a,所以PD
-a,所以PD![]() DQ≤a(6
DQ≤a(6![]() -a)=-(a-3
-a)=-(a-3![]() )2+18,即当PD=DQ=3
)2+18,即当PD=DQ=3![]() 时求得PD
时求得PD![]() DQ的最大值
DQ的最大值
试题解析:(1)∵y=x2-4x=(x-2)2-4,∴抛物线的对称轴是直线x=2,∵直线y=x+m与坐标轴的交点坐标为(-m,0),(0,m),∴交点到原点的距离相等,∴直线与坐标轴围成的三角形是等腰直角三角形,∴直线PQ与x轴所夹锐角的度数是45°.故答案为x=2;45°.(2)设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,OE>AF,S△POQ=![]() S△PAQ不成立;①当点B落在线段OA上时,如图①,
S△PAQ不成立;①当点B落在线段OA上时,如图①,
![]() ,由△OBE∽△ABF得,
,由△OBE∽△ABF得, ![]() ,∴AB=3OB,∴OB =
,∴AB=3OB,∴OB =![]() OA,由y=x2-4x得点A(4,0),∴OB=1,∴B(1,0),代入y=x+m,∴1+m=0,∴m=-1;②当点B落在线段AO的延长线上时,如图②,
OA,由y=x2-4x得点A(4,0),∴OB=1,∴B(1,0),代入y=x+m,∴1+m=0,∴m=-1;②当点B落在线段AO的延长线上时,如图②,

同理可得OB =![]() OA=2,∴B(-2,0),∴-2+m=0,∴m=2,;综上所述,当m=-1或2时,S△POQ=
OA=2,∴B(-2,0),∴-2+m=0,∴m=2,;综上所述,当m=-1或2时,S△POQ=![]() S△PAQ;
S△PAQ;
(3)①过点C作CH∥x轴交直线PQ于点H,如图③,

可得△CHQ是等腰三角形,∵![]() =45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,∴PH=
=45°+45°=90°,∴AD⊥PH,∴DQ=DH,∴PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,∴PH=![]() PM,∴当PM最大时,PH最大,∴当点P在抛物线顶点处时,PM最大,此时PM=6,∴PH的最大值为6
PM,∴当PM最大时,PH最大,∴当点P在抛物线顶点处时,PM最大,此时PM=6,∴PH的最大值为6![]() ,即PD+DQ的最大值为6
,即PD+DQ的最大值为6![]() .②由①可知:PD+DQ ≤6
.②由①可知:PD+DQ ≤6![]() ,设PD=a,则DQ ≤6
,设PD=a,则DQ ≤6![]() -a,∴PD
-a,∴PD![]() DQ ≤a(6
DQ ≤a(6![]() -a)=-a2+6
-a)=-a2+6![]() a=-(a-3
a=-(a-3![]() )2+18,∵当点P在抛物线的顶点时,a=3
)2+18,∵当点P在抛物线的顶点时,a=3![]() ,∴PD
,∴PD![]() DQ ≤18.;∴PD
DQ ≤18.;∴PD![]() DQ的最大值为18.
DQ的最大值为18.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列属于正n边形的特征的有( )
①各边相等;②各个内角相等;③各条对角线都相等;④从一个顶点可以引(n-2)条对角线;⑤从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形.
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年销售一种产品,1月份获得利润20万元,由于产品畅销,利润逐月增加,3月份的利润比2月份的利润增加4.8万元,假设该产品利润每月的增长率相同,求这个增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y=
 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是 .
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,等腰三角形有两条边分别为2,4,则等腰三角形的周长为( )
A. 6 B. 8 C. 10 D. 8或10
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个n边形的内角和是540°,那么n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(a+1,b﹣2)在第二象限,则点B(﹣a,b+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
相关试题

