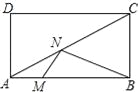
【题目】如图,在矩形ABCD中,AB=4,AD=2,点M是AB上一动点,点N是对角线AC上一动点,则MN+BN的最小值为______.
参考答案:
【答案】![]()
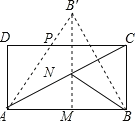
【解析】试题分析:作点B关于AC的对称点B′,过点B′作B′M⊥AB于M,交AC于N,
连接AB′交DC于P,连接BN, ∵四边形ABCD是矩形, ∴DC∥AB,
∴∠BAC=∠PCA, ∵点B关于AC的对称点是B′, ∴∠PAC=∠BAC,
∴∠PAC=∠PCA, ∴PA=PC. 令PA=x,则PC=x,PD=8-x.
在Rt△ADP中, ![]() , ∴x=
, ∴x=![]() ,
,
∵cos∠B′AM=cos∠APD, ∴AM:AB′=DP:AP, ∴AM:4=1.5:2.5,
∴AM=![]() ,∴B′M=AB′2-AM2=
,∴B′M=AB′2-AM2=![]() ,
,
∴MN+BN的最小值=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x+6=0的解是( )
A.2
B.﹣2
C.3
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】把算式-2-3-(+14)写成加法的形式是( )
A. (-2)+(-3)+(-14)B. (-2)+(-3)-(-14)
C. (-2)+(+3)+(-14)D. (-2)+(+3)+(+14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用计算器验证,下列不等式中成立的是( )
A.sin37°24′>cos37°24′+cos3°10′
B.cos45°32′>sin45°﹣sin1°12′
C.sin63°47′<cos18°21′﹣cos87°
D.2sin30°12′<sin60°24′ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC。
(1)如果AE=7cm,EB=5cm,FC=4cm,那么AF的长是多少?
(2)如果AB=10cm,AE=6cm,AF=5cm,那么FC的长是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,A、B、C、D 为矩形的四个顶点,AB=16cm,AD=
6cm,动点P、Q 分别从A、C 同时出发,点P 以3cm/s的速度向点B 移动,
一直到达点 B 为止,点 Q 以2cm/s的速度向点 D 移动.
(1)P、Q 两点从出发点出发几秒时,四边形PBCQ 的面积是33cm2?
(2)P、Q 两点从出发点出发几秒时,点P、Q 间的距离是10cm?

-
科目: 来源: 题型:
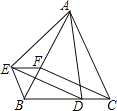
查看答案和解析>>【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
相关试题

