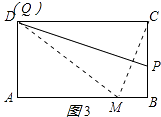
【题目】如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q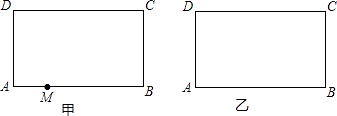
(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2 ,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离.
参考答案:
【答案】
(1)
解:如图1所示:
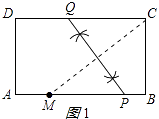
(2)
解:△MPQ是等腰三角形;理由如下:
∵四边形ABCD是矩形,
∴AB∥CD,CD=AB=10,
∴∠QCO=∠PMO,
由折叠的性质得:PQ是CM的垂直平分线,
∴CQ=MQ,OC=OM,
在△OCQ和△OMP中, 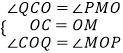 ,
,
∴△OCQ≌△OMP(ASA),
∴CQ=MP,
∴MP=MQ,
即△MPQ是等腰三角形
(3)
解:①作MN⊥CD于N,如图2所示:
则MN=AD=6,DN=AM=x,CN=10﹣x,
在Rt△MCN中,由勾股定理得:CM2=MN2+CN2,
即(2d)2=62+(10﹣x)2,
整理得:d2= ![]() x2﹣5x+34,
x2﹣5x+34,
即y= ![]() x2﹣5x+34(0≤x≤10);
x2﹣5x+34(0≤x≤10);
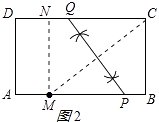
②当直线PQ恰好通过点D时,如图3所示:
则Q与D重合,DM=DC=10,
在Rt△ADM中,AM= ![]() =8,
=8,
∴BM=10﹣8=2,
∴CM= ![]() =
= ![]() =2
=2 ![]() ,
,
∴d= ![]() CM=
CM= ![]() ,
,
即点M到直线PQ的距离为 ![]() .
.
【解析】(1)作线段CM的垂直平分线即可;(2)由矩形的性质得出AB∥CD,CD=AB=10,得出∠QCO=∠PMO,由折叠的性质得出PQ是CM的垂直平分线,由线段垂直平分线的性质得出CQ=MQ,由ASA证明△OCQ≌△OMP,得出CQ=MP,得出MP=MQ即可;(3)①作MN⊥CD于N,如图2所示:则MN=AD=6,DN=AM=x,CN=10﹣x,在Rt△MCN中,由勾股定理得出(2d)2=62+(10﹣x)2 , 即可得出结果;②当直线PQ恰好通过点D时,Q与D重合,DM=DC=10,由勾股定理求出AM,得出BM,再由勾股定理求出CM,即可得出结果.本题是四边形综合题目,考查了矩形的性质、折叠的性质、线段垂直平分线的性质、全等三角形的判定与性质、等腰三角形的判定、勾股定理等知识;本题综合性强,有一定难度,证明三角形全等和运用勾股定理是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.

(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可) -
科目: 来源: 题型:
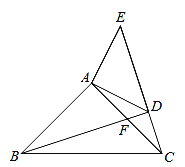
查看答案和解析>>【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
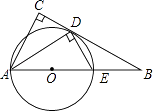
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=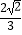 ,AE=4,求CD.
,AE=4,求CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=﹣
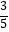 [(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( )
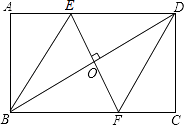
A.2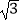
B.3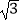
C.
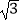
D.6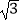
相关试题

