【题目】蜗牛从某点![]() 开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]()
(1)蜗牛最后是否回到出发点?请说明理由;
(2)蜗牛离开出发点![]() 最远时是_______厘米;
最远时是_______厘米;
(3)在爬行过程中,如果蜗牛每爬2厘米奖励一粒芝麻,求蜗牛-共得到多少粒芝麻?
参考答案:
【答案】(1)能,见解析;(2)14;(3)124
【解析】
(1)将各次的路程相加即可得到答案;
(2)分别计算每次离开的距离进行比较即可得到结果;
(3)将所有的爬行距离相加再乘以2即可得到答案.
(1)回到了原点,
∵6-4+12-8-4+13-15=0(厘米),
∴蜗牛最后回到了原点;
(2)第一次离开的距离是6厘米,
第二次离开的距离是6-4=2厘米,
第三次离开的距离是2+12=14厘米,
第四次离开的距离是14-8=4厘米,
第五次离开的距离是4-4=0厘米,
第六次离开的距离是0+13=13厘米,
第七次离开的距离是![]() 厘米,
厘米,
∴蜗牛离开出发点![]() 最远时是14厘米,
最远时是14厘米,
故答案为:14;
(3)![]() =124(粒)
=124(粒)
∴蜗牛-共得到124粒芝麻.
-
科目: 来源: 题型:
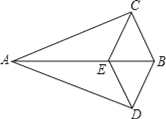
查看答案和解析>>【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.
求证:(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
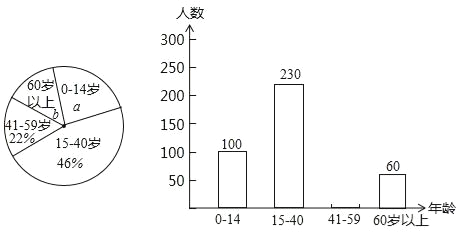
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1

(1)如果点
 表示的数互为相反数,那么点
表示的数互为相反数,那么点 表示的数是_______,点
表示的数是_______,点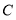 表示的数是_______;
表示的数是_______;(2)如果点
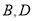 表示的数互为相反数,那么四点中,点_______表示的数的绝对值最大,请简要说明理由;
表示的数互为相反数,那么四点中,点_______表示的数的绝对值最大,请简要说明理由;(3)当点
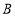 为原点时,若存在一点
为原点时,若存在一点 到点
到点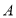 的距离是点
的距离是点 到点
到点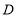 的距离的2倍,则点
的距离的2倍,则点 所表示的数是_______.
所表示的数是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EE⊥AB,垂足为F,连接DF;
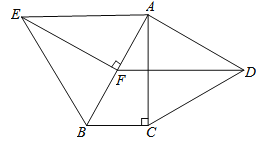
求证:(1)AC=EF;
(2)四边形ADFE是平行四边形;
(3)AC⊥DF;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位计划在春节期间组织员工
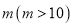 人去旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元人.两家旅行社对10人以上的团体推出了不同的优惠措施:甲旅行社对每位员工七五折优惠:乙旅行社免去一位带队员工的费用,其余员工八折优惠
人去旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元人.两家旅行社对10人以上的团体推出了不同的优惠措施:甲旅行社对每位员工七五折优惠:乙旅行社免去一位带队员工的费用,其余员工八折优惠(1)求甲、乙两家旅行社的费用分别为多少元?(用含
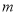 的代数式表示)
的代数式表示)(2)若该单位组织包括带队员工在内共20名员工去旅游,你认为该单位选择哪家旅行社比较优惠?并通过计算说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
相关试题

