【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
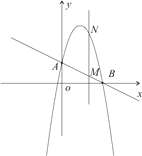
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
过A、B两点。(1)求这个抛物线的解析式;(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N。求当t 取何值时,MN有最大值?最大值是多少?
参考答案:
【答案】(1)![]() ;
;
(2) 当t=2时,MN的最大值是4.
【解析】试题分析:(1)求出点A、点B的坐标,将A、B坐标代入抛物线解析式,求出b、c的值即可;(2)将M、N的坐标用含t的式子表示,然后将MN表示为二次函数的形式,求二次函数最值即可.
试题解析:
(1)易得A(0,2),B(4,0),
将x=0,y=2代入y=-x2+bx+c得c=2,
将x=4,y=0 代入y=-x2+bx+2,得-16+4b+2=0,解得b=![]() ,
,
∴抛物线解析式为y=-x2+![]() x+2;
x+2;
(2)由题意易得M(t,- ![]() t+2),N(t,-t2+
t+2),N(t,-t2+![]() t+2),
t+2),
∴MN=-t2+![]() t+2-(-
t+2-(-![]() t+2)=-t2+
t+2)=-t2+![]() t+2+
t+2+![]() t-2=-t2+4t=-(t-2)2+4,
t-2=-t2+4t=-(t-2)2+4,
∴当t=2时,MN有最大值4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AD⊥BC,CE⊥AB,垂足分别为 D,E,AD、CE 交于点 F,若 EF=EB=5, AE=7,则 CF 的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形
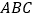 (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点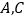 的坐标分别是
的坐标分别是 .
.(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出
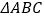 关于
关于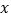 轴对称的
轴对称的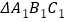 ;
;(3)请在
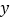 轴上求作一点
轴上求作一点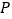 ,使
,使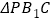 的周长最小,并写出点
的周长最小,并写出点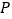 的坐标.
的坐标.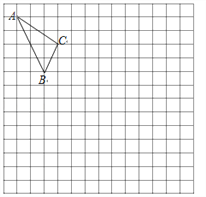
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】红富士苹果某箱上标明苹果质量为
 ,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”)
,则这箱苹果最重为__________kg,如果某箱苹果重14.95kg,则这箱苹果_________________标准.(填“符合”或“不符合”)
相关试题

