【题目】如图,直线AB与CD相交于点O,∠AOE=90°.

(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠FOB,且OE平分∠FOC,求∠EOF的度数.
参考答案:
【答案】(1)135°;(2)54°
【解析】
(1)利用OC平分∠AOE,可得∠AOC=![]() ∠AOE=
∠AOE=![]() ×90°=45°,再利用∠AOC+∠AOD=180°,即可得出.
×90°=45°,再利用∠AOC+∠AOD=180°,即可得出.
(2)由∠BOC=4∠FOB,设∠FOB=x°,∠BOC=4x°,可得∠COF=∠COB-∠BOF=3x°,根据OE平分∠COF,可得∠COE=∠EOF=![]() ∠COF=
∠COF=![]() x°,即可得出.
x°,即可得出.
(1)∵∠AOE=90°,OC平分∠AOE,
∴∠AOC=![]() ∠AOE=
∠AOE=![]() ×90°=45°,
×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°.
(2)∵∠BOC=4∠FOB,
∴设∠FOB=x°,∠BOC=4x°
∴∠COF=∠COB-∠BOF
=4x°-x°=3x°
∵OE平分∠COF
∴∠COE=∠EOF=![]() ∠COF=
∠COF=![]() x°
x°
∵![]() x+x=90°
x+x=90°
∴x=36,
∴∠EOF=![]() x°=
x°=![]() ×36°=54°
×36°=54°
即∠EOF的度数为54°.
-
科目: 来源: 题型:
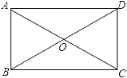
查看答案和解析>>【题目】如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个四位数,记千位上和百位上的数字之和为
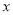 ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为 ,如果
,如果 ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,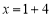 ,
, ,因为
,因为 ,所以1423是“和平数”.
,所以1423是“和平数”.(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=α,则∠BED=______.(用含α的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,能判定四边形ABCD为平行四边形的个数是( )
①AB∥CD,AD=BC ; ②AB=CD,AD=BC;③∠A=∠B,∠C=∠D; ④AB=AD,CB=CD.
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小高从家骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间x(分钟)与离家距离y(千米)的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家需要的时间是_______分钟.

相关试题

