【题目】如图所示,长方形ABCD是“阳光小区”内一块空地,已知AB=(2a+6b)米,BC=(8a+4b)米.
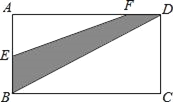
(1)该长方形ABCD的面积是多少平方米?
(2)若E为AB边的中点,DF=![]() BC,现打算在阴影部分种植一片草坪,这片草坪的面积是多少平方米?
BC,现打算在阴影部分种植一片草坪,这片草坪的面积是多少平方米?
参考答案:
【答案】(1)16a2+56ab+24b2;(2)5a2+![]() ab+
ab+![]() b2
b2
【解析】
(1)利用长方形面积计算公式即可求出答案;
(2)先求出AE、AF的长,再利用长方形面积的一半减去三角形AEF的面积即可得到阴影部分的面积.
解:(1)长方形ABCD的面积=AB×BC
=(2a+6b)(8a+4b)
=16a2+56ab+24b2;
(2)由题意得,AF=AD﹣DF=BC﹣![]() BC=(8a+4b)﹣
BC=(8a+4b)﹣![]() (8a+4b)=(6a+3b),
(8a+4b)=(6a+3b),
AE=![]() (2a+6b)=a+3b,
(2a+6b)=a+3b,
则草坪的面积=![]() ×(16a2+56ab+24b2)﹣
×(16a2+56ab+24b2)﹣![]() ×AE×AF
×AE×AF
=![]() ×(16a2+56ab+24b2)﹣
×(16a2+56ab+24b2)﹣![]() ×(a+3b)(6a+3b)
×(a+3b)(6a+3b)
=5a2+![]() ab+
ab+![]() b2.
b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是一个无理数筛选器的工作流程图.
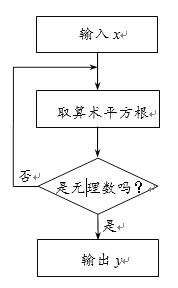
(1)当
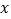 为16时,
为16时,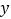 值为 ;
值为 ;(2)是否存在输入有意义的
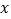 值后,却始终输不出
值后,却始终输不出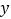 值?如果存在,写出所有满足要求的
值?如果存在,写出所有满足要求的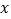 值;如果不存在,请说明理由;
值;如果不存在,请说明理由;(3)如果输入
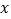 值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的
值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的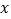 值可能是什么情况;
值可能是什么情况;(4)当输出的
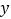 值是
值是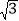 时,判断输入的
时,判断输入的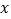 值是否唯一,如果不唯一,请写出其中的两个.
值是否唯一,如果不唯一,请写出其中的两个. -
科目: 来源: 题型:
查看答案和解析>>【题目】顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
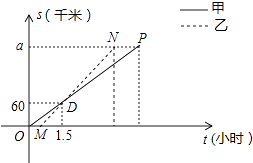
(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE的度数( )
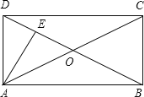
A. 30° B. 45° C. 60° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为______.
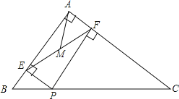
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
相关试题

