Question

【题目】

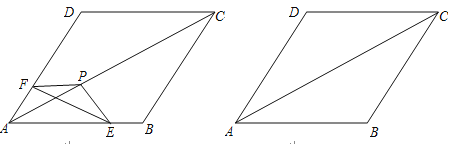
如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP=FP=6，EF=，∠BAD=60°，且AB＞．

⑴求∠EPF的大小；

⑵若AP=8，求AE+AF的值；

⑶若△EFP的三个顶点E，F，P分别在线段AB，AD，AC上运动，请直接写出AP长的最大值和最小值.

Answer 1

【答案】（1）120°；（2）；（3）AP的最大值为12，AP的最小值为6.

【解析】

试题分析：（1）如图，过点P作PG⊥EF于G，已知PE=PF=6，EF=，根据等腰三角形的性质可得FG=EG=，∠FPG=∠EPG=.在Rt△FPG中，由sin∠FPG=可求得∠FPG=60°,所以∠EPF=2∠FPG=120°.（2）作PM⊥AB于M，PN⊥AD于N，根据菱形的性质可得∠DAC=∠BAC，AM=AN，PM=PN，再利用HL证明Rt△PME≌Rt△PNF，即可得NF=ME.又因AP=10，,所以AM= AN =APcos30°==.所以AE＋AF=（AM＋ME）＋(AN－NF)=AM＋AN=.（3）如图，当△EFP的三个顶点E，F，P分别在线段AB，AD，AC上运动时，点P在，之间运动，易知，，所以AP的最大值为12，AP的最小值为6.

试题解析：（1）如图，过点P作PG⊥EF于G.

∵PE=PF=6，EF=，

∴FG=EG=，∠FPG=∠EPG=.

在Rt△FPG中，sin∠FPG=.

∴∠FPG=60°,

∴∠EPF=2∠FPG=120°.

(2)作PM⊥AB于M，PN⊥AD于N．

∵AC为菱形ABCD的对角线，

∴∠DAC=∠BAC，AM=AN，PM=PN.

在Rt△PME和Rt△PNF 中，PM=PN，PE=PF，

∴Rt△PME≌Rt△PNF

∴NF=ME.

又AP=10，,

∴AM= AN =APcos30°==.

∴AE＋AF=（AM＋ME）＋(AN－NF)=AM＋AN=.

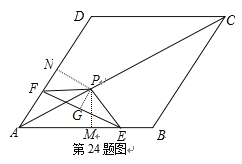
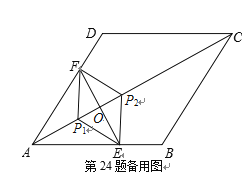
(3) 如图，当△EFP的三个顶点E，F，P分别在线段AB，AD，AC上运动时，点P在，之间运动，易知，，

∴AP的最大值为12，AP的最小值为6.