【题目】小东到学校参加毕业晚会演出,到学校时发现演出道具还放在家中,此时距毕业晚会开始还有25分钟,于是立即步行回家.同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.图中线段AB、OB表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校的路程S(米)与所用时间t分)之间的函数关系,结合图象解答下列问题.
(1)求点B坐标;
(2)求AB直线的解析式;
(3)小东能否在毕业晚会开始前到达学校?

参考答案:
【答案】(1)点B的坐标为(15,900);(2)s=﹣180t+3600;(3)小东能在毕业晚会开始前到达学校.
【解析】(1)由图象可知:父子俩从出发到相遇时花费了15分钟,设小东步行的速度为x米/分,则小东父亲骑车的速度为3x米/分,依题意得:
15(x+3x)=3600,
解得:x=60.
∴两人相遇处离学校的距离为60×15=900(米).
∴点B的坐标为(15,900);
(2)设直线AB的解析式为:s=kt+b.
∵直线AB经过点A(0,3600)、B(15,900)
∴![]()
∴直线AB的解析式为:s=﹣180t+3600;
(3)解法一:
小东取道具遇到父亲后,赶往学校的时间为: ![]() =5(分),
=5(分),
∴小东从取道具到赶往学校共花费的时间为:15+5=20(分),
∵20<25,
∴小东能在毕业晚会开始前到达学校.
解法二:
在s=﹣180t+3600中,令s=0,即﹣180t+3600=0,解得:t=20,
即小东的父亲从出发到学校花费的时间为20(分),
∵20<25,
∴小东能在毕业晚会开始前到达学校.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空题
(1)分解因式:x3-2x2y=;
(2)分解因式:2mx-6my=. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省梅州市第15题)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
 ,0),B(0,2),则点B2016的坐标[来为______________.
,0),B(0,2),则点B2016的坐标[来为______________.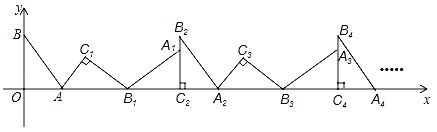
-
科目: 来源: 题型:
查看答案和解析>>【题目】1的平方根是( )
A. 1 B. -1 C. ±1 D. 不存在
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=5,ab=6,则a2+b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.3a+2b=5ab
B.2a3+3a2=5a5
C.5a2﹣4a2=1
D.3a2b﹣3ba2=0 -
科目: 来源: 题型:
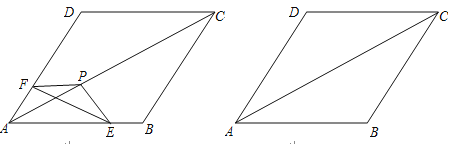
查看答案和解析>>【题目】
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=
 ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>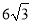 .
.⑴求∠EPF的大小;
⑵若AP=8,求AE+AF的值;
⑶若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP长的最大值和最小值.
相关试题

