【题目】如图,已知BC是△ABD的角平分线,BC=DC,∠A=∠E=30°,∠D=50°.
(1)写出AB=DE的理由;
(2)求∠BCE的度数.

参考答案:
【答案】(1)证明见解析(2)20°
【解析】
由三角形内角和定理可得∠DBA=100°,由BC是∠DBA的角平分线可得∠ABC=50°,即可证明∠ABC=∠D,通过AAS可证明△ABC≌△EDC,即可得AB=DE;(2)由∠DBC=50°,∠E=30°,根据三角形外角性质即可求出∠BCE的度数.
(1)∵∠A=30°,∠D=50°,
∴∠DBA=180°-30°-50°=100°,
∵BC是∠DBA的角平分线,
∴∠DBC=∠ABC=50°,
∴∠ABC=∠D,
∵BC=CD,∠A=∠E,∠ABC=∠D,
∴△ABC≌△EDC(AAS),
∴AB=DE.
(2)∵∠DBC=50°,∠E=30°,
∴∠BCE=∠DBC-∠E=50°-30°=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次篮球联赛初赛阶段,每队有
 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得 分, 负一场得
分, 负一场得 分,积分超过
分,积分超过 分才能获得参赛资格.
分才能获得参赛资格.(1)已知甲队在初赛阶段的积分为
 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在运动会前夕,育红中学都会购买篮球、足球作为奖品.若购买10个篮球和15个足球共花费3000元,且购买一个篮球比购买一个足球多花50元.
(1)求购买一个篮球,一个足球各需多少元?
(2)今年学校计划购买这种篮球和足球共10个,恰逢商场在搞促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1050元,则最多可购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知2x﹣y=8,求代数式[x2+y2﹣(x﹣y)2+2y(x﹣y)]÷4y的值.
(2)阅读下列材料:常用分解因式的方法有提取公因式法、公式法,但有部分多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解.过程如下:x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)这种分解因式的方法叫分组分解法.利用这种分组的思想方法解决下列问题:
已知a,b,c分别是△ABC三边的长,且2a2+b2+c2﹣2a(b+c)=0请判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


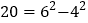
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中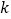 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
相关试题

