【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵矩形OBDC的边CD=1,
∴OB=1,
∵AB=4,
∴OA=3,
∴A(﹣3,0),B(1,0),
把A、B两点坐标代入抛物线解析式可得 ![]() ,解得
,解得  ,
,
∴抛物线解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
(2)
解:在y=﹣ ![]() x2﹣
x2﹣ ![]() x+2中,令y=2可得2=﹣
x+2中,令y=2可得2=﹣ ![]() x2﹣
x2﹣ ![]() x+2,解得x=0或x=﹣2,
x+2,解得x=0或x=﹣2,
∴E(﹣2,2),
∴直线OE解析式为y=﹣x,
由题意可得P(m,﹣ ![]() m2﹣
m2﹣ ![]() m+2),
m+2),
∵PG∥y轴,
∴G(m,﹣m),
∵P在直线OE的上方,
∴PG=﹣ ![]() m2﹣
m2﹣ ![]() m+2﹣(﹣m)=﹣
m+2﹣(﹣m)=﹣ ![]() m2﹣
m2﹣ ![]() m+2=﹣
m+2=﹣ ![]() (m+
(m+ ![]() )2+
)2+ ![]() ,
,
∵直线OE解析式为y=﹣x,
∴∠PGH=∠COE=45°,
∴l= ![]() PG=
PG= ![]() [﹣
[﹣ ![]() (m+
(m+ ![]() )2+
)2+ ![]() ]=﹣
]=﹣ ![]() (m+
(m+ ![]() )2+
)2+ ![]() ,
,
∴当m=﹣ ![]() 时,l有最大值,最大值为
时,l有最大值,最大值为 ![]() ;
;
(3)
解:①当AC为平行四边形的边时,则有MN∥AC,且MN=AC,如图,过M作对称轴的垂线,垂足为F,设AC交对称轴于点L,

则∠ALF=∠ACO=∠FNM,
在△MFN和△AOC中

∴△MFN≌△AOC(AAS),
∴MF=AO=3,
∴点M到对称轴的距离为3,
又y=﹣ ![]() x2﹣
x2﹣ ![]() x+2,
x+2,
∴抛物线对称轴为x=﹣1,
设M点坐标为(x,y),则|x+1|=3,解得x=2或x=﹣4,
当x=2时,y=﹣ ![]() ,当x=﹣4时,y=
,当x=﹣4时,y= ![]() ,
,
∴M点坐标为(2,﹣ ![]() )或(﹣4,﹣
)或(﹣4,﹣ ![]() );
);
②当AC为对角线时,设AC的中点为K,
∵A(﹣3,0),C(0,2),
∴K(﹣ ![]() ,1),
,1),
∵点N在对称轴上,
∴点N的横坐标为﹣1,
设M点横坐标为x,
∴x+(﹣1)=2×(﹣ ![]() )=﹣3,解得x=﹣2,此时y=2,
)=﹣3,解得x=﹣2,此时y=2,
∴M(﹣2,2);
综上可知点M的坐标为(2,﹣ ![]() )或(﹣4,﹣
)或(﹣4,﹣ ![]() )或(﹣2,2).
)或(﹣2,2).
【解析】(1)由条件可求得A、B的坐标,利用待定系数法可求得抛物线解析式;(2)可先求得E点坐标,从而可求得直线OE解析式,可知∠PGH=45°,用m可表示出PG的长,从而可表示出l的长,再利用二次函数的性质可求得其最大值;(3)分AC为边和AC为对角线,当AC为边时,过M作对称轴的垂线,垂足为F,则可证得△MFN≌△AOC,可求得M到对称轴的距离,从而可求得M点的横坐标,可求得M点的坐标;当AC为对角线时,设AC的中点为K,可求得K的横坐标,从而可求得M的横坐标,代入抛物线解析式可求得M点坐标.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用50节A,B两种型号的车厢将这批货物运至北京,已知每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型车厢,甲种货物25吨和乙种货物35吨可装满一节B型车厢,按此要求安排A,B两种车厢的节数,共有哪几种方案?请你设计出所有方案,并说明哪种方案的运费最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式
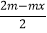 >
> x﹣1.
x﹣1.(1)当m=1时,求该不等式的解集;
(2)m取何值时,该不等式有解,并求出解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数,例如:[3.5]=3,[4]=4,[-1.5]=-2;用{a}表示大于a的最小整数,例如:{3.5}=4,{1}=2,{-2.5}=-2.解决下列问题:
(1)[-5.5]等于多少,{2.5}等于多少;
(2)若[x]=3,写出x的取值范围;若{y}=-2,写出y的取值范围.
(3)已知x,y满足方程组
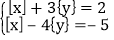 ,求x,y的取值范围.
,求x,y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼.小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,下列说法不正确的是( )
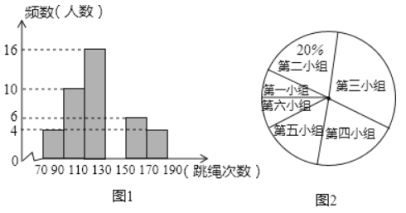
A.第四小组有10人B.本次抽样调查的样本容量为50
C.该校“一分钟跳绳”成绩优秀的人数约为480人D.第五小组对应圆心角的度数为
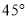
相关试题

