【题目】如图,△ABC是等边三角形,点D、E分别是BC边、AB边上的点,且BE=CD,连接AD、CE交于点F,过A作AH⊥CE于H,
(1)求证:∠BCE=∠CAD;
(2)直接写出∠CFD的度数;并写出线段AF与线段HF的数量关系.(无需解答过程)
参考答案:
【答案】
(1)
证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠ACD=60°,
在△BCE与△ACD中, 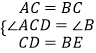 ,
,
∴△BCE≌△ACD,
∴∠BCE=∠CAD
(2)
∠CFD=60°,AF=2HF,
∵∠BCE=∠CAD,∠ACF+∠CAF=60°,
∴∠DAC+∠ACF=60°,
∵∠CFD=∠DAC+∠ACF,
∴∠CFD=60°,
∵AH⊥CE,
∴∠HAF=30°,
∴AF=2HF.
【解析】(1)由△ABC是等边三角形,于是得到AB=AC=BC,∠B=∠ACD=60°,证得△BCE≌△ACD,根据全等三角形的性质即可得到结论;(2)由(1)证得∠BCE=∠CAD,于是推出∠DAC+∠ACF=60°,根据外角的性质得到∠CFD=∠DAC+∠ACF,于是得到∠CFD=60°,根据直角三角形的性质即可得到结论.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣4,2,﹣1,3这四个数中,比﹣2小的数是( )
A.﹣4
B.2
C.﹣1
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC>AB>AC,∠ACB=50°,点D、点E是射线BA上的两个点,且满足AD=AC,BE=BC,则∠DCE的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若□ABCD中,∠A=50°,则∠C=_______°.
-
科目: 来源: 题型:
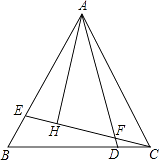
查看答案和解析>>【题目】如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠3=∠4,求证:∠5=∠6.
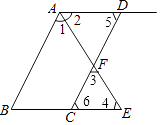
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,已知A(2x,3x+1).
(1)点A在x轴下方,在y轴的左侧,且到两坐标轴的距离相等,求x的值;
(2)若x=1,点B在x轴上,且S△OAB=6,求点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.
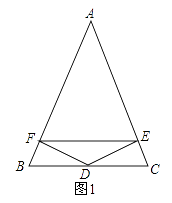
(1)求证:AE=AF;
(2)如图2,若∠BAC=60°,△ABD的面积为4,连接AD交EF于M,连接BM、CM,在不添加任何辅助线的情况下,请直接写出图中所有面积为1的三角形.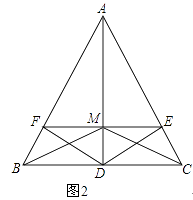
相关试题

