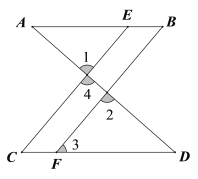
【题目】如图,已知∠1=∠2,∠B=∠C.求证:(1)AB∥CD;(2) ∠AEC=∠3.
参考答案:
【答案】(1)答案见详解,(2)答案见详解.
【解析】
(1)由∠1=∠2结合对顶角相等即可得出∠2=∠4,进而可证出CE∥BF,再根据平行线的性质可得出∠3=∠C=∠B,利用平行线的判定定理即可证出AB∥CD;
(2)由AB∥CD可得∠AEC=∠C,再根据(1)中∠B=∠C=∠3即可证得∠AEC=∠3.
证明:(1)∵∠1=∠2(已知),∠1=∠4(对顶角相等),
∴∠2=∠4(等量替换),
∴CE∥BF(同位角相等,两直线平行),
∴∠3=∠C(两直线平行,同位角相等).
又∵∠B=∠C(已知),
∴∠3=∠B(等量替换),
∴AB∥CD(内错角相等,两直线平行).
(2)∵AB∥CD(已知),
∴∠AEC=∠C(两直线平行,内错角相等).
∵∠B=∠C=∠3(由(1)可知),
∴∠AEC=∠3(等量替换).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt
 中,
中, ,分别以点A、C为圆心,大于
,分别以点A、C为圆心,大于 长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.
长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.(1)求
 ;(直接写出结果)
;(直接写出结果)(2)当AB=3,AC=5时,求
 的周长.
的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
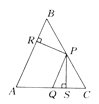
A. ①③ B. ②③ C. ①② D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△CDE均为等边三角形,且点B,C,D在同一直线上,连结AD,BE,分别交CE和AC于点G,H,连结GH.
(1)请说出AD=BE的理由;
(2)试说出△BCH≌△ACG的理由;
(3)试猜想△CGH是什么特殊的三角形,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2﹣2bx+c,当x<2时,y的值随x的增大而增大,则实数b的取值范围是( )
A.b≥﹣1
B.b≤﹣1
C.b≥﹣2
D.b≤﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】你会求(a﹣1)(a2012+a2011+a2010+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
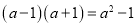 ,
,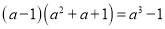 ,
,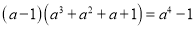 ,
,(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 .
(3)求52014+52013+52012+…+52+5+1的值.
相关试题

