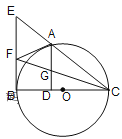
【题目】如图,A是以BC为直径的⊙O上的一点, AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E, 点F是EB的中点,连结CF交AD于点G.
(1)求证:AF是⊙O的切线;
(2)求证:AG=GD;
(3)若FB=FG,且⊙O的半径长为![]() ,求BD.
,求BD.
参考答案:
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
试题分析:(1)连接AB, OA,根据直径所对的圆周角是直角可得∠BAC=90°,∠BAE=90°,根据切线的判定与性质可证明;
(2)利用相似三角形的性质与判定可证明;
(3)过点F作FH⊥AD于点H,由等腰三角形和相似三角形的性质与判定可求解.
试题解析:(1)连接AB, OA,
∵BC是直径
∴∠BAC=90°,∠BAE=90°
∵点F是EB的中点
∴AF=BF=EF
∵AF=BF
∴∠FBA=∠FAB
∵OB=OA
∴∠OBA=∠OAB
∴∠FBD=∠FAO
∵BF是⊙O的切线
∴∠FBD=90°
∴∠FAO=90°
∴AF是⊙O的切线。
(2)∵AD⊥BC,∠FBD=90°
∴EB∥AD
∴△FBC∽△GDC, △EBC∽△ADC
∴![]() ,
,![]()
∴![]()
∵EF=FB
∴AG=GD
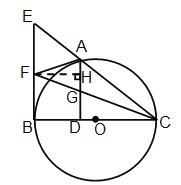
(3)过点F作FH⊥AD于点H
∵AD⊥BC, FH⊥AD
∴FH∥BC
∴∠FHG=∠GDO, ∠HFG=∠DCG
∴△HFG∽△DCG
∵AD⊥BC, FH⊥AD,EB⊥BC
∴四边形HFBD是矩形
∴FH=BD
∵FG=FB,FB=FA
∴FA=FG
∴△AFG是等腰三角形
∴![]() ,
,
∵AG=GD
∴![]()
设BD=x,则FH=x,CD=![]()
∵△HFG∽△DCG
∴![]()
∴![]()
![]()
∴BD=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:

(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果平行四边形的周长为20 cm,一边长为4 cm,则它的邻边长为____________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【题目】若10m=5,10n=3,则102m+3n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下事件中,必然发生的是( )
A.打开电视机,正在播放体育节目
B.打开数学课本,恰好翻到第88页
C.通常情况下,水加热到100℃沸腾
D.抛掷一枚均匀的硬币,恰好正面朝上 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B与反比例函数
 (k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若
(k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若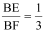 , 则
, 则 ____
____ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(x﹣y)2=x2﹣y2B.2x2+x2=3x2
C.(﹣2x2)3=8x6D.x3÷x=x3
相关试题

