【题目】已知:平面直角坐标系中,点A在y轴的正半轴上,点B在第二象限, AO= AB,∠BOX=150° .
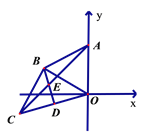
(1)试判定△ABO的形状;
(2)若BC⊥BO,BC=BO,点D为CO的中点,AC、DB交于E,求证:AE=BE+CE.
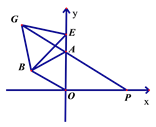
(3)如图:若点E为y轴的正半轴上一动点,以BE为边作等边△BEG,延长GA交x轴于点P,问:AP与AO之间有何数量关系,试证明你的结论.
参考答案:
【答案】(1) △AOB为等边三角形;(2)证明见解析;(3)AP=2AO,理由见解析.
【解析】试题分析:(1)根据∠BOX=150°, ∠AOX=90°,计算出∠AOB=60°,又因为AO= AB,所以可以判定△ABO是等边三角形,(2)在AC上截取AM=CE,先证∠AEB=60°,理由是根据题意可得△AOB为等边三角形, △BOC为等腰直角三角形,确定出∠ABD度数,根据AB=BC,且夹角∠BAC=∠BCA,利用SAS得到△BCM和△BAE全等,利用全等三角形的性质可得BM=BE,得到△BEM是等边三角形,得到BE=EM,由AE=EM+AM,等量代换即可求证,
(3)AP=2AO,理由是根据题意得到BG=BE,AB=OB,
利用等式的性质得到∠ABG=∠OBE=60°,利用外角的性质得到∠APO=30°,在直角三角形中,利用30度所对直角边等于斜边的一半可以得到AP=2AO.
试题解析:(1)∵OB与x轴正半轴夹角为150°,x轴⊥y轴,
∴∠AOB=150°-90°=60°,
∵AO=AB,
∴△AOB为等边三角形,
(2)在AC上截取AM=EC,可得AM+EM=CE+EM,即AE=CM,
∵△AOB为等边三角形, △BOC为等腰直角三角形,
∴∠OBC=90°,∠ABO=60°,
∵D为CO的中点,
∴BD平分∠OBC,即∠CBD=∠OBD=45°,
∴∠ABD=105°,∠ABC=150°,
∴∠BAC=∠BCA=15°,
∴∠AEB=60°,
在△ABE和△CBM中,AB=CB,∠BAE=∠BCM,AE=CM,
∴△ABE≌△CBM(SAS),
∴BM=BE,
∴△BEM为等边三角形,
∴BE=EM,
∴AE=AM+EM=CE+BE,
(3)AP=2AO,理由为:
∵△AOB与△BGE都为等边三角形,
∴BE=BG,AB=OB,∠EBG=∠OBA=60°,
∴∠EBG+∠EBA=∠OBA+∠EBA,即∠ABG=∠OBE,
在△ABG和△OBE中,AB=OB,∠ABG=∠OBE,BE=BG,
∴△ABG≌△OBE(SAS),
∴△ABG≌△OBE(SAS),
∴∠BAG=∠BOE=60°,
∴∠GAO=∠GAB+∠BAO=120°,
∵∠GAO为△AOP的外角,且∠AOP=90°,
∴∠APO=30°,
在Rt△AOP中,∠APO=30°,
则AP=2AO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①棱柱的侧面是长方形;②棱柱的侧面可能是三角形;③正方体的所有棱长都相等;④棱柱的所有侧棱长都相等.其中正确的有_____.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月24日上午9时港珠澳大桥正式通车,它是东亚建设的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,整个大桥造价超过720亿元人民币,将72000000000用科学记数法表示为( )
A.7.2×1011B.7.2×1010C.0.72×1011D.72×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个棱柱共有12个顶点,且所有侧棱长的和为120 cm,则此棱柱的每条侧棱的长为___.
-
科目: 来源: 题型:
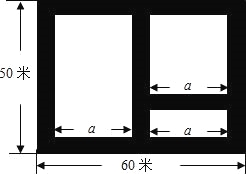
查看答案和解析>>【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
(1)设通道的宽度为x米,则a= (用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截一个几何体,其截面形状是圆,则原几何体可能为___________________
①圆柱 ②圆锥 ③球 ④正方体 ⑤长方体(请填上正确的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+3吨表示运入仓库的大米吨数, 那么运出5吨大米表示为( )
A.-3吨
B.+3吨
C.-5吨
D.+5吨
相关试题

