搜索
【题目】如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“和谐数”如（8=32﹣12，16=52﹣32，即8，16均为“和谐数”），在不超过2017的正整数中，所有的“和谐数”之和为（ ）
A. 255054 B. 255064 C. 250554 D. 255024
参考答案：
【答案】D
【解析】
由（2n+1）2﹣（2n﹣1）2=8n≤2017，解得n≤252
，可得在不超过2017的正整数中，“和谐数”共有252个，依此列式计算即可求解．
由（2n+1）2﹣（2n﹣1）2=8n≤2017，解得：n≤252，则在不超过2017的正整数中，所有的“和谐数”之和为32﹣12+52﹣32+…+5052﹣5032=5052﹣12=255024．
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在△ABC中，∠C＝2∠B，D是BC边上的一点，且AD⊥AB，E是BD的中点，连结AE.
求证：(1)∠AEC＝∠C；
(2)BD＝2AC.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，O是直线l上一点，在点O的正上方有一点A，满足OA＝3，点A，B位于直线l的同侧，且点B到直线l的距离为5，线段AB＝
，一动点C在直线l上移动．(1)当点C位于点O左侧时，且OC＝4，直线l上是否存在一点P，使得△ACP为等腰三角形？若存在，请求出OP的长；若不存在，请说明理由．
(2)连结BC，在点C移动的过程中，是否存在一点C，使得AC＋BC的值最小？若存在，请求出这个最小值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列因式分解，正确的是（ ）
A. x2y2-z2=x2（y+z）（y-z） B. -x2y+4xy-5y=-y（x2+4x+5）
C. （x+2）2-9=（x+5）（x-1） D. 9-12a+4a2=-（3-2a）2
【答案】C
【解析】解析：选项A.用平方差公式法，应为x2y2-z2=（xy+z）·（xy-z），故本选项错误.
选项B.用提公因式法，应为-x2y+ 4xy-5y=- y（x2- 4x+5），故本选项错误.
选项C.用平方差公式法，（x+2）2-9=（x+2+3）（x+2-3）=（x+5）（x-1），故本选项正确.
选项D.用完全平方公式法，应为9-12a+4a2=（3-2a）2，故本选项错误.
故选C.
点睛：(1)完全平方公式：
.(2)平方差公式：(a+b)(a-b)=
.(3)常用等价变形：
,
,
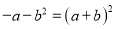.【题型】单选题
【结束】
10【题目】已知a，b，c分别是△ABC的三边长，且满足2a4+2b4+c4=2a2c2+2b2c2，则△ABC是（ ）
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连结GF，给出下列结论：①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4
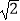，其中正确的结论个数为（ ）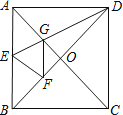 
A.2
B.3
C.4
D.5 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为
的大正方形，两块是边长都为
的小正方形，五块是长为
、宽为
的全等小矩形，且
> 
．（以上长度单位：cm）（1）观察图形，可以发现代数式
可以因式分解为 ；（2）若每块小矩形的面积为10
，四个正方形的面积和为58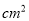
，试求图中所有裁剪线（虚线部分）长之和．
-
科目： 来源： 题型：
查看答案和解析>>【题目】中秋佳节我国有赏月和吃月饼的传统，某校数学兴趣小组为了了解本校学生喜爱月饼的情况，随机抽取了60名同学进行问卷调查，经过
统计后绘制了两幅尚不完整的统计图．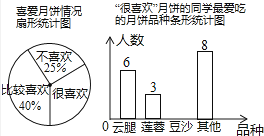
（注：参与问卷调查的每一位同学在任何一种分类统计中只有一种选择）
请根据统计图完成下列问题：
（1）扇形统计图中，“很喜欢”的部分所对应的圆心角为度；条形统计图中，喜欢“豆沙”月饼的学生有人；
（2）若该校共有学生900人，请根据上述调查结果，估计该校学生中“很喜欢”和“比较喜欢”月饼的共有人．
（3）甲同学最爱吃云腿月饼，乙同学最爱吃豆沙月饼，现有重量、包装完全一样的云腿、豆沙、莲蓉、蛋黄四种月饼各一个，让甲、乙每人各选一个，请用画树状图法或列表法，求出甲、乙两人中有且只有一人选中自己最爱吃的月饼的概率．
相关试题
