【题目】甲和乙一起做游戏,下列游戏规则对双方公平的是( )

A. 在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋中任意摸出一球,摸到红球甲获胜,摸到白球乙获胜;
B. 从标有号数1到100的100张卡片中,随意抽取一张,抽到号数为奇数甲获胜,否则乙获胜;
C. 任意掷一枚质地均匀的骰子,掷出的点数小于4则甲获胜,掷出的点数大于4则乙获胜;
D. 让小球在如图所示的地板上自由地滚动,并随机地停在某块方块上,若小球停在黑色区域则甲获胜,若停在白色区域则乙获胜
参考答案:
【答案】B
【解析】
根据概率论公式分别计算出A、B、C选项中甲获胜和乙获胜的概率,利用几何概率的计算方法计算出D选项中甲获胜和乙获胜的概率,然后比较两概率的大小判断游戏的公平性.
A.甲获胜的概率=![]() ,乙获胜的概率=
,乙获胜的概率=![]() ,而
,而![]() <
<![]() ,所以游戏规则对双方不公平,所以A选项错误.
,所以游戏规则对双方不公平,所以A选项错误.
B.甲获胜的概率=![]() ,乙获胜的概率=
,乙获胜的概率=![]() ,所以游戏规则对双方公平,所以B选项正确.
,所以游戏规则对双方公平,所以B选项正确.
C.甲获胜的概率=![]() ,乙获胜的概率=
,乙获胜的概率=![]() ,而
,而![]() ,所以游戏规则对双方不公平,所以C选项错误.
,所以游戏规则对双方不公平,所以C选项错误.
D.甲获胜的概率=![]() ,乙获胜的概率=
,乙获胜的概率=![]() ,而
,而![]() ,所以游戏规则对双方不公平,所以D选项错误.
,所以游戏规则对双方不公平,所以D选项错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2018年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生
 已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF=60°,DE、DF分别交AC、BC与E、F点。
(1)如图,若EF∥AB,求证DE=DF
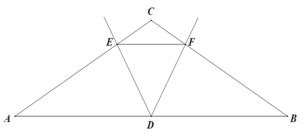
(2)如图,若EF与AB不平行,则问题(1)的结论是否成立?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定:转动两个转盘停止后,指针必须指到某一数字,否则重转.
(1)请用树状图或列表法列出所有可能的结果;
(2)若指针所指的两个数字都是方程x2-5x+6=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-5x+6=0的解时,则乙获胜,问他们两人谁获胜的概率大?请分析说明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一节数学活动课上,王老师将本班学生身高数据(精确到1厘米)出示给大家,要求同学们各自独立绘制一幅频数分布直方图,甲绘制的如图①所示,乙绘制的如图②所示,经王老师批改,甲绘制的图是正确的,乙在数据整理与绘图过程中均有个别错误.
(1)写出乙同学在数据整理或绘图过程中的错误(写出一个即可);

(2)甲同学在数据整理后若用扇形统计图表示,则159.5﹣164.5这一部分所对应的扇形圆心角的度数为 ;
(3)该班学生的身高数据的中位数是 ;
(4)假设身高在169.5﹣174.5范围的5名同学中,有2名女同学,班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手,那么恰好选中一名男同学和一名女同学当正,副旗手的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形.计算(a+b)n的结果中的各项系数依次对应杨辉三角的第(n+1)行中的每一项,如,(a+b)3=a3+3a2b+3ab2+b3,若t是(a﹣b)2019展开式中ab2018的系数,则t的值为( )
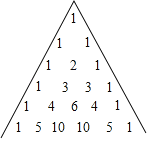
A.2018B.﹣2018C.2019D.﹣2019
相关试题

