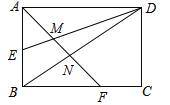
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理得到AF=![]() =
=![]() =
=![]() ,根据平行线分线段成比例定理得到,OH=
,根据平行线分线段成比例定理得到,OH=![]() AE=
AE=![]() ,由相似三角形的性质得到
,由相似三角形的性质得到![]() =
=![]() ,求得AM=
,求得AM=![]() AF=
AF=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() =
=![]() ,求得AN=
,求得AN=![]() AF=
AF=![]() ,即可得到结论.
,即可得到结论.
过F作FH⊥AD于H,交ED于O,则FH=AB=2.
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF=![]() =
=![]() =
=![]() ,
,
∵OH∥AE,
∴![]() =
=![]() ,
,
∴OH=![]() AE=
AE=![]() ,
,
∴OF=FH﹣OH=2﹣![]() =
=![]() ,
,
∵AE∥FO,∴△AME∽△FMO,
∴![]() =
=![]() ,∴AM=
,∴AM=![]() AF=
AF=![]() ,
,
∵AD∥BF,∴△AND∽△FNB,
∴![]() =
=![]() ,
,
∴AN=![]() AF=
AF=![]() ,
,
∴MN=AN﹣AM=![]() ﹣
﹣![]() =
=![]() ,故选B.
,故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
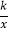 的图象与一次函数y=
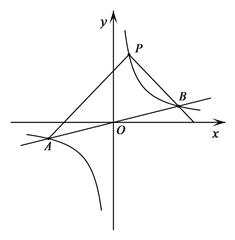
的图象与一次函数y=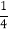 x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 的图象与y轴的正半轴交于点A,其顶点B在
的图象与y轴的正半轴交于点A,其顶点B在 轴的负半轴上,且OA=OB,对于下列结论:①
轴的负半轴上,且OA=OB,对于下列结论:①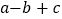 ≥0;②
≥0;② ;③关于
;③关于 的方程
的方程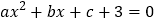 无实数根;④
无实数根;④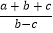 的最小值为3.其中正确结论的个数为( )
的最小值为3.其中正确结论的个数为( ) 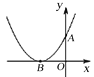
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识再现:
如果
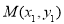 ,
,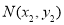 ,则线段
,则线段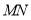 的中点坐标为
的中点坐标为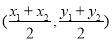 ;对于两个一次函数
;对于两个一次函数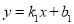 和
和 ,若两个一次函数图象平行,则
,若两个一次函数图象平行,则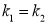 且
且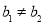 ;若两个一次函数图象垂直,则
;若两个一次函数图象垂直,则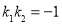 .
.提醒:在下面这个相关问题中如果需要,你可以直接利用以上知识.
在平面直角坐标系中,已知点
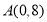 ,
,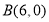 .
.(1)如图1,把直线
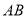 向右平移使它经过点
向右平移使它经过点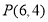 ,如果平移后的直线交
,如果平移后的直线交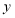 轴于点
轴于点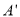 ,交x轴于点
,交x轴于点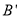 ,请确定直线
,请确定直线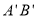 的解析式.
的解析式.(2)如图2,连接
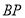 ,求
,求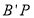 的长.
的长.(3)已知点
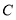 是直线
是直线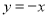 上一个动点,以
上一个动点,以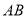 为对角线的四边形
为对角线的四边形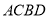 是平行四边形,当
是平行四边形,当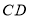 取最小值时,请在图3中画出满足条件的
取最小值时,请在图3中画出满足条件的 ,并直接写出此时
,并直接写出此时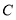 点坐标.
点坐标.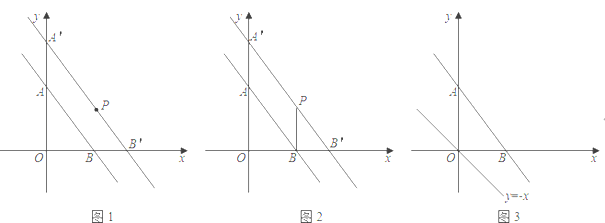
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某种产品展开图,高为3cm.
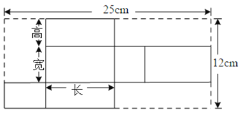
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方形 ABCD (如图 1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2 左上角正方形AEMH再作划分,得图3,则图3 中共有9个正方形;
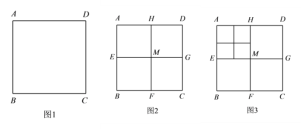
(1)若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有 个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)按这种方法能否将正方形ABCD划分成有2015个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算
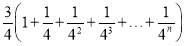 .( 直接写出答案即可)
.( 直接写出答案即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中四个直角三角形是全等的,若大正方形ABCD的面积是小正方形EFGH面积的13倍,则
 的值为______________.
的值为______________.
相关试题

