【题目】如图,反比例函数y=![]() 与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=
与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=![]() .
.
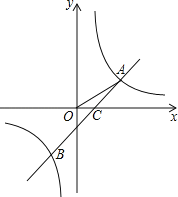
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值.
参考答案:
【答案】(1)y=![]() ,y=
,y=![]() x﹣1.(2)
x﹣1.(2)![]() .
.
【解析】
试题分析:(1)过点A作AE⊥x轴于点E,根据tanα=![]() 可得出m的值,进而得出反比例函数的解析式,根据B(﹣2,n)在反比例函数y=
可得出m的值,进而得出反比例函数的解析式,根据B(﹣2,n)在反比例函数y=![]() 的图象上得出B点坐标,再把A、B两点的坐标代入直线y=k2x+b即可得出其解析式;
的图象上得出B点坐标,再把A、B两点的坐标代入直线y=k2x+b即可得出其解析式;
(2)先求出C点坐标,再由A点坐标可得出AE的长,根据锐角三角函数的定义即可得出结论.
解:(1)过点A作AE⊥x轴于点E,
∵tan∠AOE=tanα=![]() ,
,
∴OE=4AE.
∵A(m,1),
∴AE=1,
∴OE=4,
∴A(4,1).
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴k1=4,
∴反比例函数的解析式为y=![]() .
.
∵B(﹣2,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=2,
∴B(﹣2,﹣2).
将A、B两点的坐标代入直线y=k2x+b得,
 ,解得
,解得 ,
,
∴直线AB的解析式为y=![]() x﹣1.
x﹣1.
(2)∵直线AB的解析式为y=![]() x﹣1,令y=0,则x=2,
x﹣1,令y=0,则x=2,
∴C(2,0).
∵A(4,1),
∴CE=2,AE=1,
∴tanβ=![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分
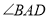 ,
, 于E,
于E, 于F,且
于F,且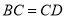 .
.
(1)求证:
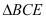 ≌
≌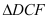 ;
;(2)若
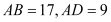 ,求AE的长.
,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P到x轴、y轴的距离分别是2和3,且点P关于y轴对称的点在第四象限,则点P的坐标是 .
-
科目: 来源: 题型:
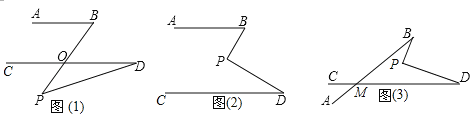
查看答案和解析>>【题目】(1)、如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD °.
(2)、如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)、在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD,AD∥BC,∠B=90,AD=6,AB=4,BC=9.

(1)求CD的长为.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】等式(x+4)0=1成立的条件是( )
A.x为有理数 B.x≠0 C.x≠4 D.x≠-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x+4y﹣3=0,那么2x16y= .
相关试题

