【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m< ![]() ;④n≤1.
;④n≤1.
则所有正确结论的序号是 .
参考答案:
【答案】①②④
【解析】解:∵抛物线过点A(﹣1,1),B(2,4), ∴ ![]() ,
,
∴b=﹣a+1,c=﹣2a+2.
∵a>0,
∴b<1,c<2,
∴结论①②正确;
∵抛物线的顶点坐标为(m,n),
∴m=﹣ ![]() =﹣
=﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴m< ![]() ,结论③不正确;
,结论③不正确;
∵抛物线y=ax2+bx+c(a>0)经过A(﹣1,1),顶点坐标为(m,n),
∴n≤1,结论④正确.
综上所述:正确的结论有①②④.
所以答案是:①②④.
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为线段AB上一点,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若AC+BC=acm,其他条件不变,直接写出线段MN的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据解答过程填空(理由或数学式)
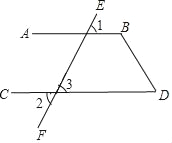
如图,已知∠1=∠2,∠D=60°,求∠B的度数.
解∵∠2=∠3( )
又∵∠1=∠2(已知),
∴∠3=∠1(等量代换)
∴ ∥ ( )
∴∠D+∠B=180°( )
又∵∠D=60°(已知),
∴∠B= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表:
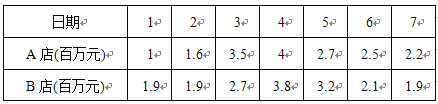
(1)要评价两家餐饮店日营业额的平均水平,你选择什么统计量?求出这个统计量;
(2)分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1)
(3)你能预测明年黄金周中哪几天营业额会比较高吗?说说你的理由.
-
科目: 来源: 题型:
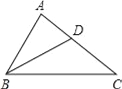
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
(1)若∠C=38°,则∠ABD= ;
(2)求证:BC=AB+AD;
(3)求证:BC2=AB2+ABAC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程
解:过点A作ED∥BC
∴∠B=∠ ,∠C=∠ .
又∵∠EAB+∠BAC+∠DAC=180°(平角定义)
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
小明受到启发,过点C作CF∥AB如图所示,请你帮助小明完成解答:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
①如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °(用含n的代数式表示)

-
科目: 来源: 题型:
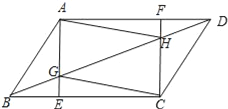
查看答案和解析>>【题目】已知:如图,在ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
求证:四边形AGCH是平行四边形.
相关试题

