【题目】设△ABC的面积为1.
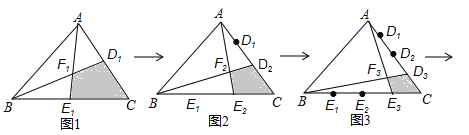
如图1,分别将AC,BC边2等分,D1,E1是其分点,连接AE1,BD1交于点F1,得到四边形CD1F1E1,其面积S1=![]() .
.
如图2,分别将AC,BC边3等分,D1,D2,E1,E2是其分点,连接AE2,BD2交于点F2,得到四边形CD2F2E2,其面积S2=![]() ;
;
如图3,分别将AC,BC边4等分,D1,D2,D3,E1,E2,E3是其分点,连接AE3,BD3交于点F3,得到四边形CD3F3E3,其面积S3=![]() ;
;
…
按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CDnEnFn,其面积S= .
参考答案:
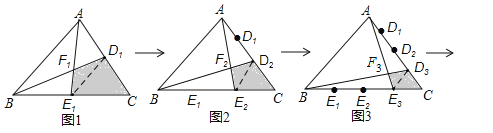
【答案】![]() .
.
【解析】
试题分析:如图所示,连接D1E1,D2E2,D3E3,∵图1中,D1,E1是△ABC两边的中点,∴D1E1∥AB,D1E1=![]() AB,∴△CD1E1∽△CBA,且
AB,∴△CD1E1∽△CBA,且![]() =
=![]() ,∴S△CD1E1=
,∴S△CD1E1=![]() S△ABC=
S△ABC=![]() ,∵E1是BC的中点,∴S△BD1E1=S△CD1E1=
,∵E1是BC的中点,∴S△BD1E1=S△CD1E1=![]() ,∴S△D1E1F1=
,∴S△D1E1F1=![]() S△BD1E1=
S△BD1E1=![]() ×
×![]() =
=![]() ,∴S1=S△CD1E1+S△D1E1F1=
,∴S1=S△CD1E1+S△D1E1F1=![]() +
+![]() =
=![]() ,同理可得:
,同理可得:
图2中,S2=S△CD2E2+S△D2E2F2=![]() =
=![]() ,图3中,S3=S△CD3E3+S△D3E3F3=
,图3中,S3=S△CD3E3+S△D3E3F3=![]() =
=![]() ,以此类推,将AC,BC边(n+1)等分,得到四边形CDnEnFn,其面积Sn=
,以此类推,将AC,BC边(n+1)等分,得到四边形CDnEnFn,其面积Sn=![]() =
=![]() ,故答案为:
,故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知am=6,an=2,则am+n的值等于 ( )
A. 8B. 12C. 36D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )

A.
 B.
B. C.
C.  D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x-8=。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数
 (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校后勤人员到一家文具店给九年级的同学购买考试用文具包,文具店规定一次购买400个以上,可享受8折优惠.若给九年级学生每人购买一个,不能享受8折优惠,需付款1936元;若多买88个,就可享受8折优惠,同样只需付款1936元.请问该学校九年级学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒).
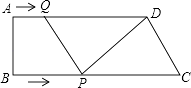
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C、D、Q、P为顶点的梯形面积等于60cm2?
相关试题

