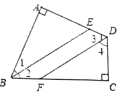
【题目】如图所示,四边形![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() 与
与![]() 不重合,则
不重合,则![]() 与
与![]() 有何位置关系?试说明理由.
有何位置关系?试说明理由.
参考答案:
【答案】BE//DF;理由见解析.
【解析】
根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行.
BE∥DF.理由如下:
∵∠A=∠C=90°(已知),
∴∠ABC+∠ADC=180°(四边形的内角和等于360°).
∵BE平分∠ABC,DF平分∠ADC,
∴![]() (角平分线的定义).
(角平分线的定义).
∴![]() (等式的性质).
(等式的性质).
又∠1+∠AEB=90°(三角形的内角和等于180°),
∴∠3=∠AEB(同角的余角相等).
∴BE∥DF(同位角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )
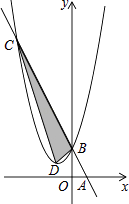
A.8:1
B.6:1
C.5:1
D.4:1 -
科目: 来源: 题型:
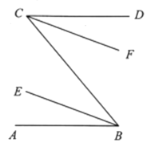
查看答案和解析>>【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)如图,已知
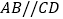 ,
, 、
、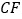 分别平分
分别平分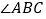 和
和 ,求证:
,求证: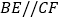 .
.证明:∵AB//CD,(已知)
∴∠ABC=∠______.(两直线平行,内错角相等)
∵__________.(已知)
∴∠EBC=
 ∠ABC,(角的平分线定义)
∠ABC,(角的平分线定义)同理,∠FCB=______.
∵∠EBC=∠FCB.(等量代换)
∴BE//CF.(____________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a0,a1,a2,a3,a4,…,满足下列条件:a0=0,a1=﹣|a0+1|,a2=﹣|a1+2|,a3=﹣|a2+3|,…,以此类推,a2019的值是( )
A. ﹣1009B. ﹣1010C. ﹣2018D. ﹣2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为
 ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.

相关试题

