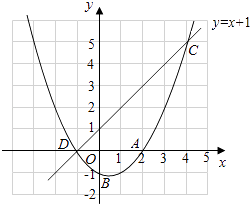
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点. 
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
参考答案:
【答案】
(1)解:∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,
∴ 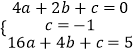 ,
,
∴a= ![]() ,b=﹣
,b=﹣ ![]() ,c=﹣1,
,c=﹣1,
∴二次函数的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣1
x﹣1
(2)解:当y=0时,得 ![]() x2﹣
x2﹣ ![]() x﹣1=0;
x﹣1=0;
解得x1=2,x2=﹣1,
∴点D坐标为(﹣1,0)
(3)解:图象如图,
当一次函数的值大于二次函数的值时,x的取值范围是﹣1<x<4.
【解析】(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;(3)画出图象,再根据图象直接得出答案.
【考点精析】本题主要考查了一次函数的图象和性质和抛物线与坐标轴的交点的相关知识点,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作为宁波市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车量的统计,结果如图:

(1)求这7天日租车量的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)共租车多少万车次;
(3)市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年租车费收入占总投入的百分率(精确到0.1%). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.

(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=
 ,反比例函数y=
,反比例函数y=  (k>0)的图象过CD的中点E.
(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用). A方法:剪6个侧面; B方法:剪4个侧面和5个底面.
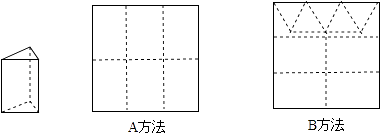
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子? -
科目: 来源: 题型:
查看答案和解析>>【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法. 我们有多少种剪法,图1是其中的一种方法:
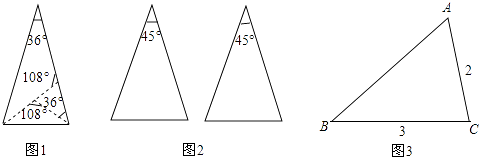
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值;
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:
方案一:直接锯一个半径最大的圆;
方案二:圆心O1、O2分别在CD、AB上,半径分别是O1C、O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.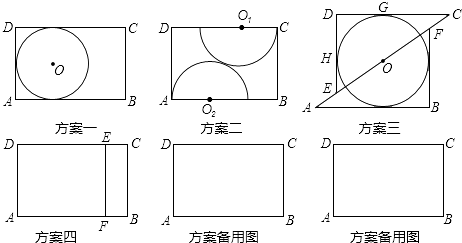
(1)写出方案一中圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=x(0<x<1),圆的半径为y.
①求y关于x的函数解析式;
②当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.
相关试题

