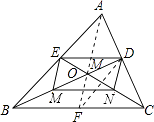
【题目】如图,△ABC中,BD、CE分别是AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点,连接DE、EM、MN、ND. 
(1)求证:四边形DEMN是平行四边形;
(2)若四边形DEMN是菱形,且BC=4cm,AC=6cm,求边AB的长.
参考答案:
【答案】
(1)证明:∵BD、CE分别是AC、AB上的中线,
∴点E为线段AB的中点,点D为线段AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,且BC=2DE.
∵点M、N分别是OB、OC的中点,
∴MN为△OBC的中位线,
∴MN∥BC,且BC=2MN.
∴DE∥MN,DE=MN,
∴四边形DEMN是平行四边形
(2)作BC边上的中线AF,交BD于M,连接DF,
∵BD、AF是边AC、BC上的中线,
∴DF∥BA,DF= ![]() BA.
BA.
∴△MDF∽△MBA,
∴ ![]() =
= ![]() ,
,
即BD=3DM,
∵四边形DEMN是菱形,且BC=4cm,AC=6cm,
∴EM=DN=MN=2cm,
∴AB=AC=6cm.
【解析】(1)由中位线定理,可得ED∥BC,MN∥BC,且都等于边长BC的一半.分析到此,此题证明即可.(2)根据三角形的中位线定理,得DF∥BA,DF= ![]() BA.根据平行得到三角形MDF相似于三角形MBA,再根据相似三角形的对应边的比相等即可求解.
BA.根据平行得到三角形MDF相似于三角形MBA,再根据相似三角形的对应边的比相等即可求解.
【考点精析】利用三角形中位线定理和平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A(﹣3,0),B(0,4),C(1,m),当△ABC是直角三角形时,m的值为 .
-
科目: 来源: 题型:
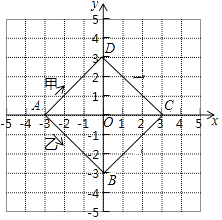
查看答案和解析>>【题目】如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(﹣3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C,点B所表示的有理数是5的相反数,按要求完成下列各小题.
(1)请在数轴上标出点B和点C;
(2)求点B所表示的有理数与点C所表示的有理数的乘积;
(3)若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.
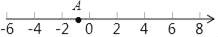
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲,乙两个区内进行了调查统计,将调查结果分为很满意,满意,不满意,很不满意四类,回收、整理好全部问卷后,得到下列不完整的统计图. 请结合图中信息,解决下列问题:

(1)参加这次调查的总人数为人,其中调查结果为“满意”的人数是人,调查结果为“很不满意”的人数占总人数的百分比为 , 扇形图中“不满意”部分对应扇形的圆心角为度.
(2)兴趣小组准备从调查结果为“很不满意”的4位市民中随机选择2位进行回访,已知这4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
(1)a+b= ,
 = ;
= ;(2)判断b+c,a﹣c,(b+c)(a﹣b)的符号;
(3)判断
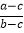 的符号.
的符号.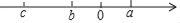
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出点A′,B′,C′的坐标;
(3)求△ABC的面积.

相关试题

