【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
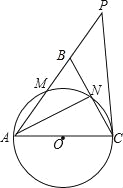
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
参考答案:
【答案】(1)证明见解析;(2)4.
【解析】
试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;
(2)利用锐角三角函数,即勾股定理即可.
试题解析:(1)∵∠ABC=∠ACB,
∴AB=AC,
∵AC为⊙O的直径,
∴∠ANC=90°,
∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,
∵∠CAB=2∠BCP,
∴∠BCP=∠CAN,
∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,
∵点D在⊙O上,
∴直线CP是⊙O的切线;
(2)如图,作BF⊥AC
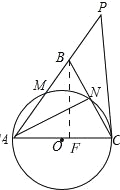
∵AB=AC,∠ANC=90°,
∴CN=![]() CB=
CB=![]() ,
,
∵∠BCP=∠CAN,sin∠BCP=![]() ,
,
∴sin∠CAN=![]() ,
,
∴![]()
∴AC=5,
∴AB=AC=5,
设AF=x,则CF=5﹣x,
在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,
在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,
∴25﹣x2=2O﹣(5﹣x)2,
∴x=3,
∴BF2=25﹣32=16,
∴BF=4,
即点B到AC的距离为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究圆的有关性质时,我们曾做过这样的一个操作“将一张圆形纸片沿着它的任意一条直径翻折,可以看到直径两侧的两个半圆互相重合”.由此说明( )
A. 圆是中心对称图形,圆心是它的对称中心
B. 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴
C. 圆的直径互相平分
D. 垂直弦的直径平分弦及弦所对的弧
-
科目: 来源: 题型:
查看答案和解析>>【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1)l1和l2哪一条是描述小凡的运动过程,说说你的理由;
(2)小凡和小光谁先出发,先出发了多少分钟?
(3)小凡与小光谁先到达图书馆,先到了多少分钟?
(4)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)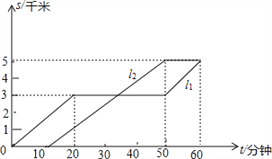
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG,其中不正确的结论的个数为( )
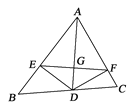
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A. k≤﹣4 B. k≥﹣4 C. k≤4 D. k>4
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“直角三角形两锐角互余”的逆命题是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3b﹣ab=_________.
相关试题

