【题目】如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1 , y1)平移后的对应点为P′(x1+6,y1+4).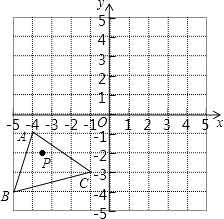
(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标.
(3)求△A′B′C′的面积.
参考答案:
【答案】
(1)解:如图所示;
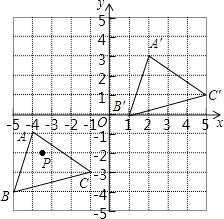
(2)解:由图可知,A′(2,3)、B′(1,0)、C′(5,1)

(3)解:S△A′B′C′=3×4﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×1×4﹣
×1×4﹣ ![]() ×2×3
×2×3
=12﹣ ![]() ﹣2﹣3
﹣2﹣3
= ![]()
【解析】①根据△ABC中任意一点平移后的对应点为P'(x1+6,y1+4)可以知道△ABC应向右平移6个单位,向上平移4个单位,由此作出△A'B'C'即可;
②根据各点在坐标系中的位置写出点A'、B'、C'的坐标即可;
③根据△A'B'C'的面积等于长方形的面积减去三个角上三角形的面积即可.
【考点精析】解答此题的关键在于理解坐标与图形变化-平移的相关知识,掌握新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,
然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,
②﹣①得,3S﹣S=39﹣1,即2S=39﹣1,
所以S=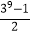 .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x(x+2)=x+2
(2)x2﹣4x﹣12=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=
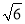 ,EF=2,∠H=120°,则DN的长为( )
,EF=2,∠H=120°,则DN的长为( )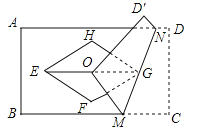
A.
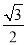 B.
B.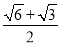 C.
C.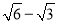 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“平行四边形的对角线互相平行”是________事件.(填“必然”、“随机”、“不可能”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=6,点E在边CD上,DE=
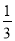 DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是 .
DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是 .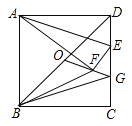
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A.四个角相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线垂直的四边形是菱形
D.对角线垂直的平行四边形是菱形
相关试题

