【题目】将一副直角三角板如图1摆放在直线AD上(直角三角板OBC和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC不动,将三角板MON绕点O以每秒10°的速度顺时针旋转,旋转时间为t秒 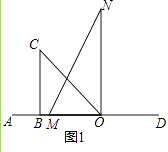
(1)当t=秒时,OM平分∠AOC?如图2,此时∠NOC﹣∠AOM=°; 
(2)继续旋转三角板MON,如图3,使得OM、ON同时在直线OC的右侧,猜想∠NOC与∠AOM有怎样的数量关系?并说明理由; 
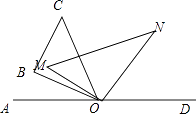
(3)若在三角板MON开始旋转的同时,另一个三角板OBC也绕点O以每秒5°的速度顺时针旋转,当OM旋转至射线OD上时同时停止,(自行画图分析)
①当t=秒时,OM平分∠AOC?
(4)②请直接写出在旋转过程中,∠NOC与∠AOM的数量关系.
参考答案:
【答案】
(1)2.25;45
(2)解:∠NOC﹣∠AOM=45°,
∵∠AON=90°+10t,
∴∠NOC=90°+10t﹣45°
=45°+10t,
∵∠AOM=10t,
∴∠NOC﹣∠AOM=45°
(3)3
(4)解:②∠NOC﹣ ![]() ∠AOM=45°.
∠AOM=45°.
∵∠AOB=5t,∠AOM=10t,∠MON=90°,∠BOC=45°,
∵∠AON=90°+∠AOM=90°+10t,∠AOC=∠AOB+∠BOC=45°+5t,
∴∠NOC=∠AON﹣∠AOC=90°+10t﹣45°﹣5t=45°+5t,
∴∠NOC﹣ ![]() ∠AOM=45°.
∠AOM=45°.
【解析】解:(1)∵∠AOC=45°,OM平分∠AOC,
∴∠AOM= ![]() =22.5°,
=22.5°,
∴t=2.25秒,
∵∠MON=90°,∠MOC=22.5°,
∴∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°;
故答案为:2.25,45;
·(3)①∵∠AOB=5t,∠AOM=10t,
∴∠AOC=45°+5t,
∵OM平分∠AOC,
∴∠AOM= ![]() AOC,
AOC,
∴10t= ![]() (45°+5t),
(45°+5t),
∴t=3秒,
故答案为:3.
(1)根据角平分线的定义得到∠AOM= ![]() =22.5°,于是得到t=2.25秒,由于∠MON=90°,∠MOC=22.5°,即可得到∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°;(2)根据题意得∠AON=90°+10t,求得∠NOC=90°+10t﹣45°=45°+10t,即可得到结论;(3)①根据题意得∠AOB=5t,∠AOM=10t,求得∠AOC=45°+5t,根据角平分线的定义得到∠AOM=
=22.5°,于是得到t=2.25秒,由于∠MON=90°,∠MOC=22.5°,即可得到∠NOC﹣∠AOM=∠MON﹣∠MOC﹣∠AOM=45°;(2)根据题意得∠AON=90°+10t,求得∠NOC=90°+10t﹣45°=45°+10t,即可得到结论;(3)①根据题意得∠AOB=5t,∠AOM=10t,求得∠AOC=45°+5t,根据角平分线的定义得到∠AOM= ![]() AOC,列方程即可得到结论;(4)②根据角的和差即可得到结论.
AOC,列方程即可得到结论;(4)②根据角的和差即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“等腰三角形的两底角相等”这个命题的条件是_________;结论________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】点O在直线AB上,点A1 , A2 , A3 , …在射线OA上,点B1 , B2 , B3 , …在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,以每秒1个单位长度的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动,即从OA1B1B2→A2…按此规律,则动点M到达A10点处所需时间为( )秒.
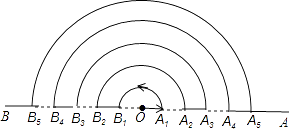
A.10+55π
B.20+55π
C.10+110π
D.20+110π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上,且BC=4厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发在直线上运动,则经过秒时线段PQ的长为5厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正六边形的每个外角都是30°,那么这个多边形的内角和为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个有理数
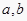 ,如果
,如果  ,且
,且 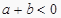 ,那么( )
,那么( )
A.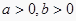
B.
C. 异号
异号
D. 异号,且负数的绝对值较大
异号,且负数的绝对值较大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果a与-1互为相反数,则|a+2|等于( )
A. 2 B. -2 C. 3 D. -3
相关试题

