【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )
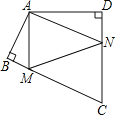
A. 80° B. 90° C. 100° D. 130°
参考答案:
【答案】C
【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
解:作DA延长线A A″,
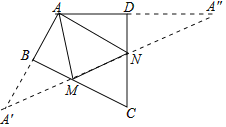
∵∠DAB=130°,
∴∠HAA′=50°,
∴∠AA′M+∠A″=∠HAA′=50°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×50°=100°,
故选C.
“点睛”本题考查的是轴对称-最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M、N的位置是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
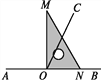
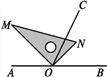
图1 图2
(1)如图1,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的平分线,求∠BON和∠CON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=20 cm,直线AB上有一点C,且BC=6 cm,点M是线段AB的中点,点N是线段BC的中点,则MN=____________ cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程x+2y=7的正整数解有( )
A.2个
B.3个
C.4个
D.无数个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON为锐角.下列说法:①∠MOP=
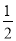 ∠MON;②∠MOP=∠NOP=
∠MON;②∠MOP=∠NOP=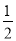 ∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( )
∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2xy3)2= ,(﹣2a)3﹣(﹣a)(3a)2=
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读解题过程,回答问题.
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
相关试题

