【题目】永嘉县绿色和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我县收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放![]() 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为![]() 元,试写出
元,试写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
参考答案:
【答案】(1)、y=![]() (
(![]() ≤
≤![]() ≤110,且
≤110,且![]() 为整数);(2)、50天;(3)、存放100天后出售这批香菇可获得最大利润30000元.
为整数);(2)、50天;(3)、存放100天后出售这批香菇可获得最大利润30000元.
【解析】
试题分析:(1)、根据根据销售总金额=单价×数量得出函数解析式;(2)、根据利润=销售额-进货成本-各种费用求出x的值,得出答案;(3)、将利润的函数解析式化成顶点式,然后根据函数的性质得出最大值.
试题解析:(1)、由题意得![]() 与
与![]() 之间的函数关系式为y=
之间的函数关系式为y=![]() =
=![]() (
(![]() ≤
≤![]() ≤110,且
≤110,且![]() 为整数)
为整数)
(2)、由题意得:![]() -10×2000-340
-10×2000-340![]() =22500
=22500
解方程得:![]() =50 ,
=50 , ![]() =150(不合题意,舍去),
=150(不合题意,舍去),
李经理想获得利润2250元需将这批香菇存放50天后出售。
(3)、设存放x天后可获得利润为![]() 元,由题意得
元,由题意得
W=![]() -10 ×2000-340
-10 ×2000-340![]()
![]() ,
,
∴当x![]() 时,
时,![]() , 100天<110天,
, 100天<110天,
∴存放100天后出售这批香菇可获得最大利润30000元.
-
科目: 来源: 题型:
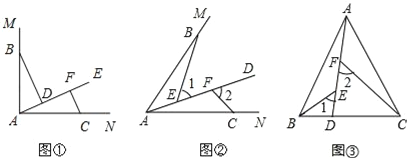
查看答案和解析>>【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠A是锐角,且sinA=cosA,那么∠A=( )
A.30°
B.45°
C.60°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三内角的度数的比为1:1:2,则此三角形( )
A. 锐角三角形 B. 钝角三角形 C. 等边三角形 D. 等腰直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠α=50°17′,∠α的余角的大小为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示, AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】按程序x平方+x÷x﹣2x进行运算后,结果用x的代数式表示是 .(填入运算结果的最简形式)
相关试题

