【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:①点G是BC中点;②FG=FC;③S△FGC=![]() .其中正确的是( )
.其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
参考答案:
【答案】B
【解析】分析:先求出DE、CE的长,再根据翻折的性质可得AD=AF,EF=DE,∠AFE=∠D=90°,再利用“HL”证明Rt△ABG和Rt△AFG全等,根据全等三角形对应边相等可得BG=FG,再设BG=FG=x,然后表示出EG、CG,在Rt△CEG中,利用勾股定理列出方程求出x=![]() ,从而可以判断①正确;根据∠AGB的正切值判断∠AGB≠60°,从而求出∠CGF≠60°,△CGF不是等边三角形,FG≠FC,判断②错误;先求出△CGE的面积,再求出EF:FG,然后根据等高的三角形的面积的比等于底边长的比求解即可得到△FGC的面积,判断③正确.
,从而可以判断①正确;根据∠AGB的正切值判断∠AGB≠60°,从而求出∠CGF≠60°,△CGF不是等边三角形,FG≠FC,判断②错误;先求出△CGE的面积,再求出EF:FG,然后根据等高的三角形的面积的比等于底边长的比求解即可得到△FGC的面积,判断③正确.
详解:∵正方形ABCD中,AB=3,CD=3DE,
∴DE=![]() ×3=1,CE=3-1=2,
×3=1,CE=3-1=2,
∵△ADE沿AE对折至△AFE,
∴AD=AF,EF=DE=1,∠AFE=∠D=90°,
∴AB=AF=AD,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
设BG=FG=x,则EG=EF+FG=1+x,CG=3-x,
在Rt△CEG中,EG2=CG2+CE2,
即(1+x)2=(3-x)2+22,
解得,x=![]() ,
,
∴CG=3-![]() =
=![]() ,
,
∴BG=CG=![]() ,
,
即点G是BC中点,故①正确;
∵tan∠AGB= ![]() =2,
=2,
∴∠AGB≠60°,
∴∠CGF≠180°-60°×2≠60°,
又∵BG=CG=FG,
∴△CGF不是等边三角形,
∴FG≠FC,故②错误;
△CGE的面积=![]() CGCE=
CGCE=![]() ×
×![]() ×2=
×2=![]() ,
,
∵EF:FG=1:![]() =2:3,
=2:3,
∴S△FGC=![]() ,故③正确;
,故③正确;
综上所述,正确的结论有①③.
故选B.
-
科目: 来源: 题型:
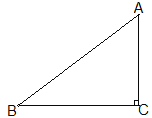
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).
(1)若点P在BC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.

(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)用含有x、y的代数式表示右图中“囧”的面积;
(2)当
 时,求此时“囧”的面积.
时,求此时“囧”的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距50千米.星期天上午8:00小聪同学在父亲陪同下骑山地车从甲地前往乙地.2小时后,小明的父亲骑摩托车沿同一路线也从甲地前往乙地,他们行驶的路程y(千米)与小聪行驶的时间x(小时)之间的函数关系如图所示,小明父亲出发 小时时,行进中的两车相距8千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2.
求证:(1)BE=DF;(2)AF∥CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.
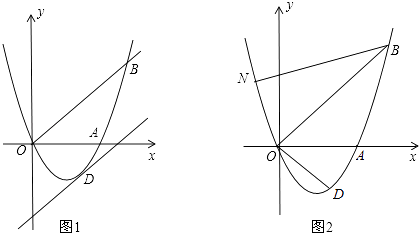
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
相关试题

