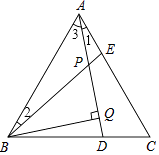
【题目】如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP⊥AD于P点. 
求证:
(1)△BAE≌△ACD;
(2)∠BQP=60°;
(3)BQ=2PQ.
参考答案:
【答案】
(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
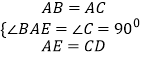 ,
,
∴△ABE≌△CAD(SAS)
(2)∵△ABE≌△CAD
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°
(3)∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.
【解析】(1)由AB=AC,∠BAE=∠C,AE=CD,即可证明.(2)根据三角形的外角的性质,∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,即可证明.(3)利用直角三角形30度性质即可解决问题.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,已知AD∥BC,若要判定四边形ABCD是平行四边形,则还需要满足的条件是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.
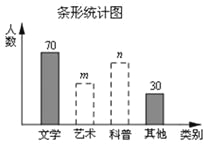
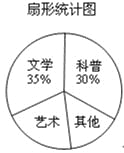
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学杨老师为学校购买运动会的奖品后,回学校向总务处童老师交账说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1200元,现在找还余下的118元.” 童老师算了一下,说:“你肯定搞错了.”
(1)童老师为什么说他搞错了?请你用已学过方程的知识帮童老师向杨老师解释清楚;
(2)杨老师连忙清点购买的物品,发现在另外商场还买了一个笔记本,但笔记本的单价在小票上已经模糊不清,只能辨认出应为小于10元的整数,请问:笔记本的单价可能为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意列出方程组:
(1)明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,问明明两种邮票各买了多少枚?
(2)将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?
-
科目: 来源: 题型:
查看答案和解析>>【题目】比﹣4小2的数是( )
A.﹣1B.﹣2C.﹣6D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
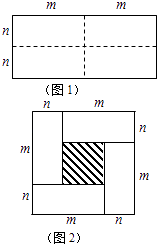
(1)请写出图2中阴影部分的面积:;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?代数式:(m+n)2 , (m﹣n)2 , mn.;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求a﹣b的值.
相关试题

