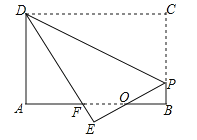
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则![]() 的值为( ).
的值为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】
根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP(AAS),根据全等三角形的性质可得出OE=OB、EF=BP,设EF=x,则BP=x、DF=4﹣x、BF=PC=3﹣x,进而可得出AF=1+x.在Rt△DAF中,利用勾股定理可求出x的值,即可得出答案.
根据折叠,可知:△DCP≌△DEP,∴DC=DE=4,CP=EP.
在△OEF和△OBP中,∵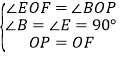 ,∴△OEF≌△OBP(AAS),∴OE=OB,EF=BP.
,∴△OEF≌△OBP(AAS),∴OE=OB,EF=BP.
设EF=x,则BP=x,DF=DE﹣EF=4﹣x.
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC﹣BP=3﹣x,∴AF=AB﹣BF=1+x.
在Rt△DAF中,AF2+AD2=DF2,即(1+x)2+32=(4﹣x)2,解得:x=0.6,∴DF=4﹣x=3.4,∴![]() .
.
故选C.
-
科目: 来源: 题型:
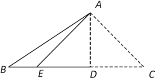
查看答案和解析>>【题目】如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=10,BE=2,则AB2-AC2的值为 ______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,
 是直角,OE平分
是直角,OE平分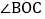 .
.
 若
若 ,则
,则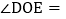 ______;若
______;若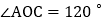 ,则
,则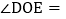 ______;
______;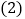 若
若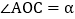 ,则
,则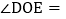 ______
______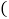 用含
用含 的式子表示
的式子表示 ,请说明理由;
,请说明理由;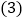 在
在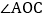 的内部有一条射线OF,满足
的内部有一条射线OF,满足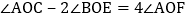 ,试确定
,试确定 与
与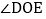 的度数之间的关系,并说明理由.
的度数之间的关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求完成画图和填空:
(1)作
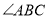 的角平分线
的角平分线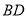 ;
;(2)作出边
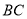 的中垂线
的中垂线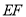 ,垂足为
,垂足为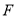 ,交
,交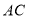 于点
于点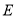 ;
;(3)过点
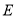 作边
作边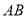 的平行线,交
的平行线,交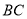 于点
于点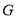 ;
;(4)点
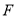 到边
到边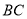 的距离是_____________.
的距离是_____________.(要求:尺规作图,保留作图痕迹,不写作法,写出结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.

(1)求证:OE=OF;
(2)若BC=2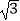 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=-2x+4,完成下列问题:
(1)画出此函数的图像;
(2)将函数y1的图像向下平移2个单位,得到函数y2的图像,直接写出函数y2的表达式;
(3)当x___时,y2>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?

相关试题

