【题目】已知菱形ABCD的边长为5,∠DAB=60°.将菱形ABCD绕着A逆时针旋转得到菱形AEFG,设∠EAB=α,且0°<α<90°,连接DG、BE、CE、CF.
(1)如图(1),求证:△AGD≌△AEB;
(2)当α=60°时,在图(2)中画出图形并求出线段CF的长;
(3)若∠CEF=90°,在图(3)中画出图形并求出△CEF的面积.

参考答案:
【答案】(1)见解析;(2)5![]() ;(3)
;(3)![]()
【解析】试题分析:(1)利用AD=AB,AG=AE,∠GAD=∠EAB(SAS)证明△AGD≌△AEB即可;
(2)当α=60°时,AE与AD重合,作DH⊥CF于H.由已知可得∠CDF=120°,DF=DC=5.在Rt△CDH中,CH=DCsin60°,继而求出CF的长;
(3)当∠CEF=90°时,延长CE交AG于M,连接AC,∠CEF=90°,只需求出EC的长,又EC=MC﹣ME.在Rt△AME和Rt△AMC中求解MC和ME的长即可.
试题解析:解:(1)∵菱形ABCD绕着点A逆时针旋转得到菱形AEFG,∴AG=AD,AE=AB,∠GAD=∠EAB=α.∵四边形AEFG是菱形,∴AD=AB,∴AG=AE,∴△AGD≌△AEB.
(2)解法一:如图(1),当α=60°时,AE与AD重合,作DH⊥CF于H.由已知可得∠CDF=120°,DF=DC=5,∴∠CDH=![]() ∠CDF=60°,CH=
∠CDF=60°,CH=![]() CF.
CF.
在Rt△CDH中,∵CH=DCsin60°=5×![]() =
=![]() ,∴CF=2CH=5
,∴CF=2CH=5![]() .
.
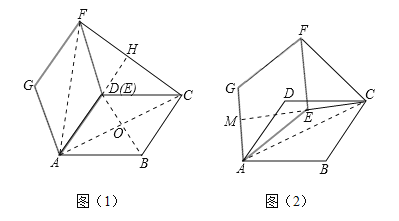
解法二:如图(1),当α=60°时,AE与AD重合,连接AF、AC、BD、AC与BD交于点O.
由题意,知AF=AC,∠FAC=60°,∴△AFC是等边三角形,∴FC=AC.
由已知,∠DAO=![]() ∠BAD=30°,AC⊥BD,∴AO=ADcos30°=
∠BAD=30°,AC⊥BD,∴AO=ADcos30°=![]() ,∴AC=2AO=5
,∴AC=2AO=5![]() ,∴FC=AC=5
,∴FC=AC=5![]() .
.
(3)如图(2),当∠CEF=90°时,延长CE交AG于M,连接AC.
∵四边形AEFG是菱形,∴EF∥AG.
∵∠CEF=90°,∴∠GME=90°,∴∠AME=90°.
在Rt△AME中,AE=5,∠MAE=60°,∴AM=AEcos60°=![]() ,EM=AEsin60°=
,EM=AEsin60°=![]() .
.
在Rt△AMC中,易求AC=5![]() ,∴MC=
,∴MC=![]() =
=![]() ,∴EC=MC﹣ME=
,∴EC=MC﹣ME=![]() ﹣
﹣![]() (
(![]() ﹣
﹣![]() ),∴S△CEF=
),∴S△CEF=![]() ECEF=
ECEF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列方程,属于一元一次方程的有( )
①x﹣2=
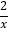 ;②0.5x=1;③
;②0.5x=1;③ =8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
=8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 A、B 在数轴上表示的数分别为﹣12 和 8,两只蚂蚁 M、N 分别 从 A、B 两点同时出发,相向而行.M 的速度为 2 个单位长度/秒,N 的速度为 3 个单位长度/秒.
(1)运动 秒钟时,两只蚂蚁相遇在点 P;点 P 在数轴上表示的数 是 ;
(2)若运动 t 秒钟时,两只蚂蚁的距离为 10,求出 t 的值(写出解题过程).

-
科目: 来源: 题型:
查看答案和解析>>【题目】有三个有理数x,y,z,若x=
 ,且x与y互为相反数,y是z的倒数.
,且x与y互为相反数,y是z的倒数.(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z,这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算:xy﹣yn﹣(y﹣z)2019的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(
 ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=30°,点D在△ABC外,且BD=2.连AD、CD,则△ACD的周长最小值为( )

A. 1B.
 C. 2D. 2
C. 2D. 2
-
科目: 来源: 题型:
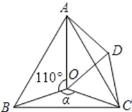
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
相关试题

