【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( ) 
A.1
B.![]()
C.4﹣2 ![]()
D.3 ![]() ﹣4
﹣4
参考答案:
【答案】C
【解析】解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,
∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,
在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4 ![]() ,
,
∴BE=BD﹣DE=4 ![]() ﹣4,
﹣4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF= ![]() BE=
BE= ![]() ×(4
×(4 ![]() ﹣4)=4﹣2
﹣4)=4﹣2 ![]() .
.
故选:C.
根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的 ![]() 倍计算即可得解.
倍计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AE平分∠BAD , ∠1=15°.

(1)求∠2的度数.
(2)求证:BO=BE . -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+4x﹣5的图象的对称轴为( )
A.x=﹣4
B.x=4
C.x=﹣2
D.x=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图.点D是Rt△ABC斜边BC的中点,⊙O是△ABD的外接圆,交AC于点F. DE平分∠ADC,交AC于点E.
求证:DE是⊙O的切线;
若CE=4,DE=2,求⊙O的直径.
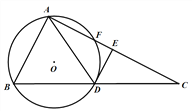
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市最高气温是33℃,最低气温是24℃,则该市气温t(℃)的变化范围是()
A. t>33 B. t≤24 C. 24<t<33 D. 24≤t≤33
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上与原点的距离小于8的点对应的x满足( )
A. ﹣8<x<8 B. x<﹣8或x>8 C. x<8 D. x>8
相关试题

