【题目】为做好“创文创卫”工作,某县城进行道路改造,由A、B两个施工队施工,已知由A施工队单独完成所有工程需要20天.若在A、B两个施工队共同施工6天后,A施工队有事撤出工程,剩下的工程由B施工队单独施工15天才完成.
(1)求B施工队单独完成所有工程需要多少天?
(2)若施工开始后,要求B施工队施工不能超过18天,要完成该工程,A施工队至少需要施工多少天才能撤出工程?
参考答案:
【答案】
(1)解:设B工程队单独完成所有工程需要x天,依题意得:
( ![]() +
+ ![]() )×6+
)×6+ ![]() =1,
=1,
解得:x=30,
经检验,x=30是原方程的解.
则B工程队单独完成所有工程需要30天.
(2)解:设A工程队至少要工作y天才能撤出工程,依题意得:
(1﹣ ![]() )÷
)÷ ![]() ≤18,
≤18,
解得:y≥8,
则A工程队至少要工作8天才能撤出工程.
【解析】(1)设B工程队单独完成所有工程需要x天,由A、B两个施工队共同施工6天后,A施工队有事撤出工程,剩下的工程由B施工队单独施工15天才完成.列出方程求解并检验即可;(2)设A工程队至少要工作y天才能撤出工程,由工作总量-A队的y天工作量的差除以B的工作效率≤18,得出不等式求解即可。
【考点精析】通过灵活运用分式方程的应用,掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示.

根据图像回答下列问题:
(1)小明家离图书馆的距离是________千米;
(2)小明在图书馆看书的时间为________小时;
(3)小明去图书馆时的速度是________千米/小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂需要在规定时间内生产1400个某种零件,该工厂按一定速度加工5天后,发现按此速度加工下去会延期10天完工,于是又抽调了一批工人投入这种零件的生产,使工作效率提高了50%,结果如期完成加工任务.
(1)求该工厂前5天每天生产多少个这种零件;
(2)求规定时间是多少天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王教授和他的孙子小强星期天一起去爬山,来到山脚下,小强让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分钟)的关系(小强开始爬山时开始计时),请看图回答下列问题:
(1)爷爷比小强先上了多少米?山顶离山脚多少米?
(2)谁先爬上山顶?小强爬上山顶用了多少分钟?
(3)图中两条线段的交点表示什么意思?这时小强爬山用时多少?离山脚多少米?
(4)直角坐标系中的横轴和纵轴上的单位长度取得不一致,这对问题的结论有影响吗?允许这样做吗?

-
科目: 来源: 题型:
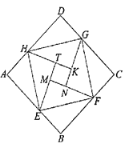
查看答案和解析>>【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由“弦图”变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )

A.
 B. 5C. 6D. 9
B. 5C. 6D. 9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠B=∠D=50°,点E、F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.

(1)∠CAF= °;
(2)若平行移动CD,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动CD的过程中,是否存在某种情况,使∠AFB=∠ACD?若存在,求出∠ACD度数;若不存在,说明理由.
-
科目: 来源: 题型:
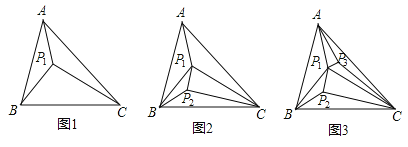
查看答案和解析>>【题目】若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()
A.n·180°B.(n+2)·180°C.(2n-1)·180°D.(2n+1)·180°
相关试题

