【题目】操作实践
(1)操作1:将矩形ABCD沿对角线AC折叠(如图1),猜想重叠部分是什么图形?并验证你的猜想.连结BE与AC有什么位置关系?
(2)操作2:折叠矩形ABCD,让点B落在对角线AC上(如图2),若AD=4,AB=3,请求出线段CE的长度.

参考答案:
【答案】(1)△AFC是等腰三角形.(2)CE=2.5.
【解析】
试题分析:(1)由矩形的性质可知AD∥BC,从而得到∠FAC=∠ACB,由翻折的性质可知∠ACB=∠ACF,于是得到∠FAC=∠FCA,故此可得到△AFC为等腰三角形;
(2)先依据勾股定理求得AC=5,由翻折的性质可知BE=EF,AF=AB=3,可求得FC=2,设EC=x,则BE=EF=4﹣x,最后在△EFC中由勾股定理可求得EC的长.
解:(1)∵四边形ABCD为矩形,
∴AD∥BC.
∴∠FAC=∠ACB.
由翻折的性质可知;∠ACB=∠ACF,
∴∠FAC=∠FCA.
∴AF=FC.
∴△AFC是等腰三角形.
(2)在Rt△ABC中,由勾股定理得:AC=![]() =5.
=5.
∵由翻折的性质可知:BE=EF,AF=AB=3.
∴FC=2,设EC=x,则BE=EF=4﹣x.
在Rt△EFC中,由勾股定理可知;EF2+FC2=EC2,即(x﹣4)2+22=x2.
解得:x=2.5.
∴CE=2.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m+n=5, mn=6。求mn-m-n的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖南省邵阳市第7题)一元二次方程2x2﹣3x+1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数
众数
中位数
方差
甲
8
8
0.4
乙
9
3.2
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠A=36°,DE是AB的垂直平分线,DE交AB于点D,交AC于点E,连接BE.下列结论①BE平分∠ABC;②AE=BE=BC;③△BEC周长等于AC+BC;④E点是AC的中点.其中正确的结论有 (填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在三角形ABC中,∠C=90°,AD是三角形ABC的角平分线,AB=AC+CD.
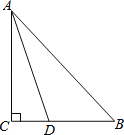
(1)求证:AC=BC;
(2)若BD=
 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图案中,是轴对称图形的是( )
A.
 B.
B. C.
C. D.
D.
相关试题

