【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.
参考答案:
【答案】解:(1)政府没出台补贴政策前,这种蔬菜的收益额为3000×800=2400000(元)
(2)设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为:
y=kx+800,z=k1x+3000,
分别把点(50,1200),(100,2700)代入得,
50k+800=1200,100k1+3000=2700,
解得:k=8,k1=﹣3,
种植亩数与政府补贴的函数关系为:y=8x+800
每亩蔬菜的收益与政府补贴的函数关系为z=﹣3x+3000(x>0)
(3)由题意:
w=yz=(8x+800)(﹣3x+3000)
=﹣24x2+21600x+2400000
=﹣24(x﹣450)2+7260000,
∴当x=450,即政府每亩补贴450元时,总收益额最大,为7260000元.
【解析】(1)根据题意可知直接计算这种蔬菜的收益额为3000×800=2400000(元);
(2)设种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式分别为:y=kx+800,z=k1x+3000,并根据图象上点的坐标利用待定系数法求函数的解析式即可;
(3)表示出蔬菜的总收益w(元)与x之间的关系式,w=﹣24x2+21600x+2400000,利用二次函数最值问题求最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) -26-(-15) (2)(+7)+(-4)-(-3)-14
(3)(-3)×
 ÷(-2)×(-
÷(-2)×(- ) (4)-(3-5)+32×(-3)
) (4)-(3-5)+32×(-3)(5)(﹣
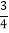 +
+ ﹣
﹣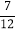 +
+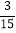 )÷
)÷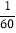 (6)- 32 -(﹣2)2+1.
(6)- 32 -(﹣2)2+1. -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果第一天以2元/斤的价格卖出a斤,第二天以1.5元/斤的价格卖出b斤第三天以1.2元/斤的价格卖出c斤,求:
(1)这三天一共卖出水果多少斤?
(2)这三天一共卖得多少钱?
(3)这三天平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=1,DC=2,点P是AB上的动点,则PC+PD的最小值为 .
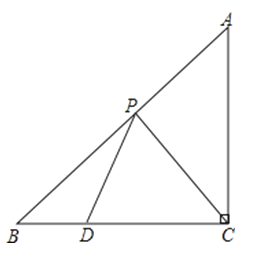
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处时,四边形AECF是矩形?并说出你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

相关试题

