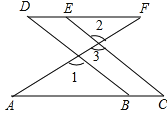
【题目】如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
参考答案:
【答案】因为∠l=∠2(已知)
∠2=∠3(对顶角相等)
所以∠l=∠3(等量代换)………………………………………………………2分
所以BD∥CE(同位角相等,两直线平行)……………………………………4分
所以∠C=∠DBA(两直线平行,同位角相等)………………………………6分
又因为∠C=∠D(已知)
所以∠DBA=∠D(等量代换)…………………………………………………8分
所以DF∥AC(内错角相等,两直线平行)………………………………………9分
所以∠A=∠F(两直线平行,内错角相等)…………………………………………10分
【解析】试题分析:根据对顶角的性质得到BD∥CE的条件,然后根据平行线的性质得到∠B=∠C,已知∠C=∠D,则得到满足AB∥EF的条件,再根据两直线平行,内错角相等得到∠A=∠F.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

-
科目: 来源: 题型:
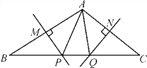
查看答案和解析>>【题目】如图所示,MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为12,求BC的长;
(2)∠BAC=105°,求∠PAQ的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:


如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,AO⊥BC于点O,点F是线段AO上的点(与A,O不重合),∠EAF=90°,AE=AF,连接FE,FC,BE,BF.
(1)求证:BE=BF;
(2)如图②,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.求证:△AGC∽△KGB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各问题中,两个变量之间的关系不是反比例函数的是( )
A. 小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系。
B. 菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系。
C. 一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的密度
 之间的关系。
之间的关系。D. 压力为600N时,压强p与受力面积S之间的关系。
相关试题

