【题目】使得函数值为零的自变量的值称为函数的零点。例如,对于函数![]() ,令
,令![]() =0,可得
=0,可得![]() =1,我们就说1是函数
=1,我们就说1是函数![]() 的零点。 己知函数
的零点。 己知函数![]() (
(![]() 为常数)。
为常数)。
(1)当![]() =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论![]() 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为![]() 和
和![]() ,且
,且![]() ,此时函数图象与
,此时函数图象与![]() 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线![]() 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
参考答案:
【答案】(1)![]() 和
和![]() ;(2)证明见解析;(3)AM的解析式为
;(2)证明见解析;(3)AM的解析式为![]()
【解析】
试题分析:(1)根据题中给出的函数的零点的定义,将m=0代入y=x2-2mx-2(m+3),然后令y=0即可解得函数的零点;
(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可;
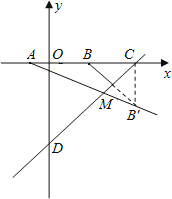
(3)根据题中条件求出函数解析式进而求得A、B两点坐标,个、作点B关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB最小时,直线AM的函数解析式.
试题解析:(1)当![]() =0时,该函数为
=0时,该函数为![]() ,令
,令![]() =0,可得
=0,可得![]() ,
,
∴当![]() =0时,求该函数的零点为
=0时,求该函数的零点为![]() 和
和![]() 。
。
(2)令![]() =0,得△=
=0,得△=![]() ,
,
∴无论![]() 取何值,方程
取何值,方程![]() 总有两个不相等的实数根。
总有两个不相等的实数根。
即无论![]() 取何值,该函数总有两个零点
取何值,该函数总有两个零点
(3)依题意有![]() ,
,![]()
由![]() 得
得![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴函数的解析式为![]() 令
令![]() =0,解得
=0,解得![]() 。
。
∵点A在点B左侧,∴A(![]() ),B(4,0)。
),B(4,0)。
作点B关于直线![]() 的对称点B’,连结AB’,则AB’与直线
的对称点B’,连结AB’,则AB’与直线![]() 的交点就是满足条件的M点。易求得直线
的交点就是满足条件的M点。易求得直线![]() 与
与![]() 轴、
轴、![]() 轴的交点分别为C(10,0),D(0,10)。
轴的交点分别为C(10,0),D(0,10)。
连结CB’,则∠BCD=45°,∴BC=CB’=6,∠B’CD=∠BCD=45°。
∴∠BCB’=90°,即B’(![]() )。设直线AB’的解析式为
)。设直线AB’的解析式为![]() ,则
,则
![]() ,解得
,解得![]() ∴直线AB’的解析式为
∴直线AB’的解析式为![]() ,
,
即AM的解析式为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式-2(x-3)>1的自然数解是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校规定学生的体育成绩由三部分组成;体育技能测试占50%,体育理论测试占20%,体育课外活动表现30%,甲同学的上述三部分成绩依次为96分,85分,90分,则甲同学的体育成绩为分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A、任何有理数都有倒数 B、互为倒数的两个数的积为1
C、互为倒数的两个数同号 D、1和-1互为负倒数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
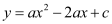 (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
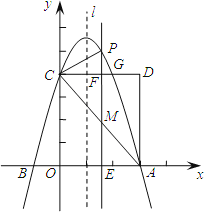
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.(1)求抛物线的解析式;
(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动,分别交x轴于点E,交CD于点F,交AC于点M,交抛物线于点P,若点M的横坐标为m,请用含m的代数式表示PM的长;
(3)在(2)的条件下,连结PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△AEM相似?若存在,求出此时m的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x与-3的差为1,则x的值是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程x+2y=12的正整数解有( )组.
A. 5 B. 6 C. 7 D. 无数
相关试题

