【题目】为响应“低碳生活”的号召,李明决定每天骑自行车上学,有一天李明骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后李明继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(千米),则y与t(15<t≤23)的函数关系为________.
参考答案:
【答案】y=100t-500(15<t≤23)
【解析】
由题意可知,李明骑车的速度为100米/分钟,由此可知他从家到学校共用去了23分钟,其中自行车出故障前行驶了10分钟,自行车修好后行驶了8分钟,由此可知当![]() 时,y与t的函数关系为:
时,y与t的函数关系为:![]() .
.
∵车修好后,李明用8分钟骑行了800米,且骑车过程是匀速行驶的,
∴李明整个上学过程中的骑车速度为:100米/分钟,
∴在自行车出故障前共用时:1000÷100=10(分钟),
∵修车用了5分钟,
∴当![]() 时,是指小明车修好后出发前往学校所用的时间,
时,是指小明车修好后出发前往学校所用的时间,
∴由题意可得:![]() (
(![]() ),
),
化简得:![]() (
(![]() ).
).
故答案为:![]() (
(![]() ).
).
-
科目: 来源: 题型:
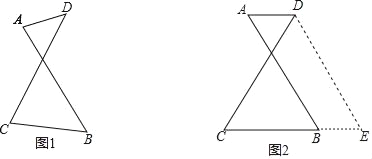
查看答案和解析>>【题目】如图1有两条长度相等的相交线段AB、CD,它们相交的锐角中有一个角为60°,为了探究AD、CB与CD(或AB)之间的关系,小亮进行了如下尝试:
(1)在其他条件不变的情况下使得AD∥BC,如图2,将线段AB沿AD方向平移AD的长度,得到线段DE,然后联结BE,进而利用所学知识得到AD、CB与CD(或AB)之间的关系: ;(直接写出结果)
(2)根据小亮的经验,请对图1的情况(AD与CB不平行)进行尝试,写出AD、CB与CD(或AB)之间的关系,并进行证明;
(3)综合(1)、(2)的证明结果,请写出完整的结论: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).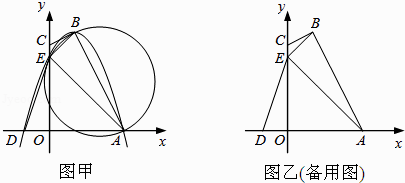
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:如图1,点
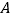 ,
, 在直线
在直线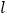 的同侧,在直线
的同侧,在直线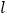 上找一点
上找一点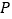 ,使得
,使得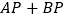 的值最小.小明的思路是:如图2,作点
的值最小.小明的思路是:如图2,作点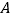 关于直线
关于直线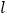 的对称点
的对称点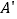 ,连接
,连接 ,则
,则 与直线
与直线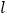 的交点
的交点 即为所求.
即为所求.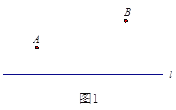
请你参考小明同学的思路,探究并解决下列问题:
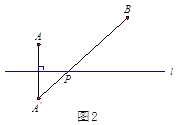
(1)如图3,在图2的基础上,设
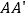 与直线
与直线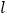 的交点为
的交点为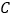 ,过点
,过点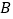 作
作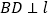 ,垂足为
,垂足为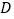 . 若
. 若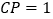 ,
,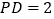 ,
,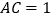 ,写出
,写出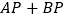 的值为____________;
的值为____________;(2)将(1)中的条件“
 ”去掉,换成“
”去掉,换成“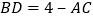 ”,其它条件不变,写出此时
”,其它条件不变,写出此时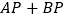 的值 ___________;
的值 ___________;(3)求
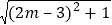 +
+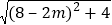 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2016年4月份用电量的调查结果:
居民(户)
1
2
3
4
月用电量(度/户)
30
42
50
51
那么关于这10户居民月用电量的说法错误的是( )
A.中位数是50
B.众数是51
C.平均数是46.8
D.方差是42 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论: ①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③a﹣b+c>0;④当y>0时,x的取值范围是﹣1≤x<3;
⑤当x<0时,y随x增大而增大
其中正确的结论有( )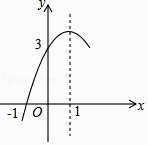
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一般情况下
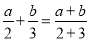 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: 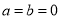 .我们称使得
.我们称使得 成立的一对数
成立的一对数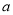 ,
, 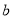 为“相伴数对”,记为
为“相伴数对”,记为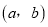 .
.(1)若
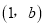 是“相伴数对”,求
是“相伴数对”,求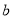 的值;
的值;(2)写出一个“相伴数对”
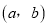 ,其中
,其中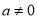 且
且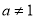 ;
;(3)若
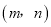 是“相伴数对”,求代数式
是“相伴数对”,求代数式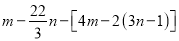 的值.
的值.
相关试题

