【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AE是经过A点的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,CE=2,BD=6,则DE的长为.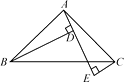
参考答案:
【答案】4
【解析】∵BD⊥AE,
∴∠BDA=90°,
∴∠ABD+∠BAD=90°,
又∠BAC=90°,
∴∠CAD+∠BAD=90°,
∴∠ABD=∠CAD,
在△ABD和△CAE中,
∴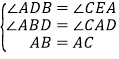 ,
,
∴△ABD≌△CAE,
又∵CE=2,BD=6,
∴BD=AE=6,AD=CE=2,
∴DE=AE-AD=BD-CE=6-2=4.
所以答案是:4.
【考点精析】根据题目的已知条件,利用余角和补角的特征的相关知识可以得到问题的答案,需要掌握互余、互补是指两个角的数量关系,与两个角的位置无关.
-
科目: 来源: 题型:
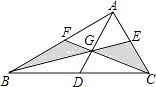
查看答案和解析>>【题目】如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数a,b,c满足|a-
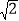 |+
|+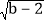 =
=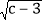 +
+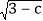 .
.(1)求a,b,c;
(2)若满足上式的a,c为等腰三角形的两边,求这个等腰三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】细心观察图形,认真分析各式,然后解答问题.
OA22=
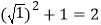 ,
, ;
;OA32=12+
 ,
, ;
;OA42=12+
 ,
, …
…(1)请用含有n(n是正整数)的等式表示上述变规律:OAn2等于多少;Sn等于多少.
(2)求出OA10的长.
(3)若一个三角形的面积是
 ,计算说明他是第几个三角形?
,计算说明他是第几个三角形?(4)求出S12+S22+S32+…+S102的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD= 120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
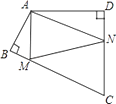
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
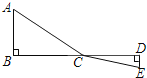
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式
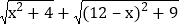 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,AB=AC,BC=8,∠BAC=120°,作AD⊥BC于点D,AD=
 AB,点E为边AC上的中点,点P为BC上一动点,则PA+PE的最小值为_______.
AB,点E为边AC上的中点,点P为BC上一动点,则PA+PE的最小值为_______.
相关试题

