【题目】关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0.
(1)有两个不相等的实数根,求m的取值范围;
(2)若x1,x2是方程的两根且x12+x22=6,求m值.
参考答案:
【答案】(1)m<1;(2)![]() .
.
【解析】试题分析:(1)由方程有两个不相等的实数根结合根的判别式,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;
(2)根据根与系数的关系结合x12+x22=6,可得出关于m的一元二次方程,解之即可得出m的值,再结合(1)即可确定m的值.
试题解析:解:(1)∵方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根,∴△=[2(m﹣2)]2﹣4(m2﹣3m+3)=﹣4m+4>0,∴m<1.
(2)∵x1,x2是方程x2+2(m﹣2)x+m2﹣3m+3=0的两根,∴x1+x2=﹣2(m﹣2),x1x2=m2﹣3m+3.
∵x12+x22=6,∴(x1+x2)2﹣2x1x2=6,即[﹣2(m﹣2)]2﹣2(m2﹣3m+3)=6,解得:m1= ![]() (舍去),m2=
(舍去),m2= ![]() ,∴m的值为
,∴m的值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务,分为A、B、C、D四种型号,它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示:

根据以上信息,下列判断错误的是( )
A. 其中的D型帐篷占帐篷总数的10%
B. 单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍
C. 单独生产A型帐篷与单独生产D型帐篷的天数相等
D. 单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
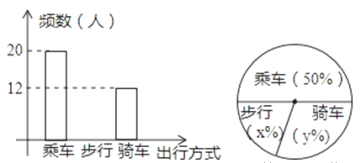
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
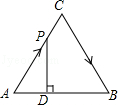
A.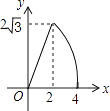
B.
C.
D.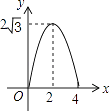
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、
 、
、 ;
;(3)如图3,A、B、C是小正方形的顶点,求∠ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=
 c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+
 cx+b=0必有实数根;
cx+b=0必有实数根;若x=1是“勾系一元二次方程”ax+
 cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是 ,求△ABC面积.
,求△ABC面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
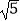 cm,且tan∠EFC=
cm,且tan∠EFC=  ,则矩形ABCD的周长是 .
,则矩形ABCD的周长是 . 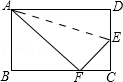
相关试题

