【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
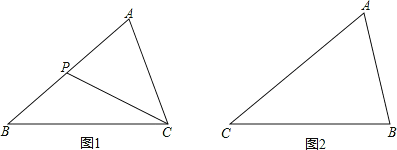
如图1,在△ABC中,P是边AB上的一点,联结CP.
要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.
请回答:
(1)王华补充的条件是____________________,或_________________.
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.
参考答案:
【答案】∠ACP=∠B(或∠APC=∠ACB),或AC2=APAB;(1)∠ACP=∠B(或∠APC=∠ACB);或AC2=APAB;理由见解析;(2)50°.
【解析】
试题分析:(1)由∠A=∠A,当∠ACP=∠B,或∠APC=∠ACB;或![]() 时,△ACP∽△ABC;
时,△ACP∽△ABC;
(2)延长AB到点D,使BD=BC,连接CD,由已知条件得出证出![]() ,由∠A=∠A,证出△ACB∽△ADC,得出对应角相等∠ACB=∠D,再由等腰三角形的性质和三角形内角和定理得出∠ACB+∠BCD+∠D+∠A=180°,得出∠ACB=50°即可.
,由∠A=∠A,证出△ACB∽△ADC,得出对应角相等∠ACB=∠D,再由等腰三角形的性质和三角形内角和定理得出∠ACB+∠BCD+∠D+∠A=180°,得出∠ACB=50°即可.
试题解析:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或![]() ,即AC2=APAB时,△ACP∽△ABC;
,即AC2=APAB时,△ACP∽△ABC;
(1)王华补充的条件是:∠ACP=∠B(或∠APC=∠ACB);或AC2=APAB;理由如下:
∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或![]() ,即AC2=APAB时,△ACP∽△ABC;
,即AC2=APAB时,△ACP∽△ABC;
(2)延长AB到点D,使BD=BC,连接CD,如图所示:
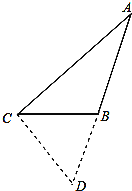
∵AC2=AB2+ABBC=AB(AB+BC)=AB(AB+BD)=ABAD,
∴![]() ,
,
又∵∠A=∠A,∴△ACB∽△ADC,
∴∠ACB=∠D,
∵BC=BD,
∴∠BCD=∠D,
在△ACD中,∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于点
轴交于点 ,交
,交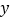 轴于点
轴于点 ,直线
,直线 过点
过点 与
与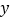 轴交于点
轴交于点 ,与抛物线的另一个交点为
,与抛物线的另一个交点为 ,作
,作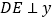 轴于点
轴于点 .设点
.设点 是直线
是直线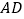 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点 、
、 重合),过点
重合),过点 作
作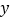 轴的平行线,交直线
轴的平行线,交直线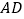 于点
于点 ,作
,作 于点
于点 .
.
(1)填空:
 __________,
__________, __________,
__________, __________;
__________;(2)探究:是否存在这样的点
 ,使四边形
,使四边形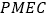 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;(3)设
 的周长为
的周长为 ,点
,点 的横坐标为
的横坐标为 ,求
,求 与
与 的函数关系式,并求出
的函数关系式,并求出 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,AD=2
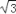 ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )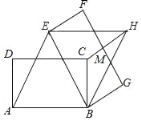
A.
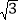 B. 2 C.
B. 2 C. 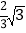 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】Windows2000下有一个有趣的“扫雷”游戏.如图是“扫雷”游戏的一部分,说明:图中数字2表示在以该数字为中心的周边8个方格中有2个地雷,小旗表示该方格已被探明有地雷.现在还剩下
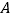 、
、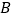 、
、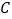 三个方格未被探明,其他地方为安全区(包括有数字的方格),则
三个方格未被探明,其他地方为安全区(包括有数字的方格),则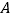 、
、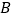 、
、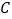 三个方格中有地雷概率最大的方格是( )
三个方格中有地雷概率最大的方格是( )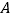
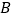
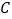
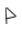
2
2
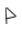
A. A B. B C. C D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量是 ,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18

-
科目: 来源: 题型:
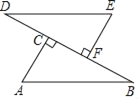
查看答案和解析>>【题目】如图,D、C、F、B四点在一条直线上,AB=DE,AC⊥BD,EF⊥BD,垂足分别为点C、点F,CD=BF.
求证:(1)△ABC≌△EDF;
(2)AB∥DE.
-
科目: 来源: 题型:
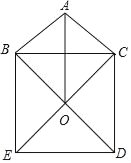
查看答案和解析>>【题目】如图,在△ABC中,AB=4,AC=3,以BC为边在三角形外作正方形BCDE,连接BD,CE交于点O,则线段AO的最大值为_____.
相关试题

