【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB= ![]() ,反比例函数y=
,反比例函数y= ![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
A.60
B.80
C.30
D.40
参考答案:
【答案】D
【解析】解:过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,如图所示.
设OA=a,BF=b,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB= ![]() ,∴AM=OAsin∠AOB=
,∴AM=OAsin∠AOB= ![]() a,OM=
a,OM= ![]() =
= ![]() a,∴点A的坐标为(
a,∴点A的坐标为( ![]() a,
a, ![]() a).∵点A在反比例函数y=
a).∵点A在反比例函数y= ![]() 的图象上,∴
的图象上,∴ ![]() a×
a× ![]() a=
a= ![]() =48,
=48,
解得:a=10,或a=﹣10(舍去).
∴AM=8,OM=6.
∵四边形OACB是菱形,
∴OA=OB=10,BC∥OA,
∴∠FBN=∠AOB.
在Rt△BNF中,BF=b,sin∠FBN= ![]() ,∠BNF=90°,∴FN=BFsin∠FBN=
,∠BNF=90°,∴FN=BFsin∠FBN= ![]() b,BN=
b,BN= ![]() =
= ![]() b,∴点F的坐标为(10+
b,∴点F的坐标为(10+ ![]() b,
b, ![]() b).∵点B在反比例函数y=
b).∵点B在反比例函数y= ![]() 的图象上,∴(10+
的图象上,∴(10+ ![]() b)×
b)× ![]() b=48,解得:b=
b=48,解得:b= ![]() ,或b=
,或b= ![]() (舍去).∴FN=
(舍去).∴FN= ![]() ,BN=
,BN= ![]() ﹣5,MN=OB+BN﹣OM=
﹣5,MN=OB+BN﹣OM= ![]() ﹣1.S△AOF=S△AOM+S梯形AMNF﹣S△OFN=S梯形AMNF=
﹣1.S△AOF=S△AOM+S梯形AMNF﹣S△OFN=S梯形AMNF= ![]() (AM+FN)MN=
(AM+FN)MN= ![]() (8+
(8+ ![]() )×(
)×( ![]() ﹣1)=
﹣1)= ![]() ×(
×( ![]() +1)×(
+1)×( ![]() ﹣1)=40.
﹣1)=40.
故选D.
过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,设OA=a,BF=b,通过解直角三角形分别找出点A、F的坐标,结合反比例函数图象上点的坐标特征即可求出a、b的值,通过分割图形求面积,最终找出△AOF的面积等于梯形AMNF的面积,利用梯形的面积公式即可得出结论.本题考查了反比例函数与一次函数交点的问题、解直角三角形、梯形的面积公式以及反比例函数图象上点的坐标特征,解题的关键是求出S梯形AMNF . 本题属于中档题,难度不大,但数据较繁琐,解决该题型题目时,通过分割图形求面积法找出所求三角形的面积与梯形面积相等是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
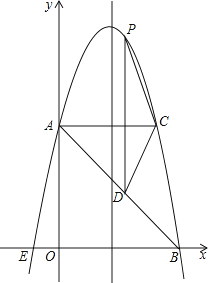
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行与y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求回答问题:

(1)已知:△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A=60°(如图①).求证:EB=AD;
(2)若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)若将(1)中的“若∠A=60°”改为“若∠A=90°”,其它条件不变,则 的值是多少?(直接写出结论,不要求写解答过程)
的值是多少?(直接写出结论,不要求写解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )

A.16cm
B.18cm
C.20cm
D.21cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: , 使△AEH≌△CEB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年6月15日是父亲节,某商店老板统计了这四年父亲节当天剃须刀销售情况,以下是根据该商店剃须刀销售的相关数据所绘制统计图的一部分.
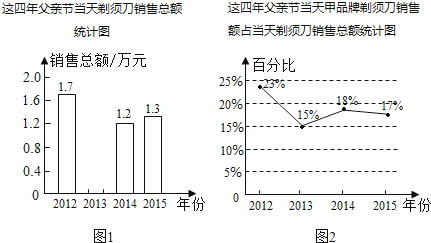
请根据图1、图2解答下列问题:
(1)近四年父亲节当天剃须刀销售总额一共是5.8万元,请将图1中的统计图补充完整;
(2)计算该店2015年父亲节当天甲品牌剃须刀的销售额. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:
 .
.
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆桥?请说明理由.
相关试题

