【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0.
(1)当k为何值时,此方程有实数根;
(2)若此方程的两个实数根x1、x2满足|x1|+|x2|=3,求k的值.
参考答案:
【答案】(1)当k≤![]() 时,此方程有实数根;(2)k的值为0.
时,此方程有实数根;(2)k的值为0.
【解析】
试题分析:(1)根据判别式的意义得到△=(2k﹣3)2﹣4(k2+1)≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2k﹣3,x1x2=k2+1>0,则可判断x1、x2同号,然后去绝对值,当x1+x2=3,即2k﹣3=3;当﹣(x1+x2)=3,即﹣(2k﹣3)=3,然后分别解关于k的方程即可.
解:(1)若方程有实数根,
则△=(2k﹣3)2﹣4(k2+1)≥0,
∴k≤![]()
∴当k≤![]() 时,此方程有实数根;
时,此方程有实数根;
(2)根据题意得x1+x2=2k﹣3,x1x2=k2+1>0,
则x1、x2同号,
当x1>0,x2>0,则x1+x2=3,即2k﹣3=3,解得k=3,
当k=3时,原方程无实数根,舍去,
当x1<0,x2<0,则﹣(x1+x2)=3,即﹣(2k﹣3)=3,解得k=0,
即k的值为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3a-b)(3a+b)-(a2+b2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是△ABC内一点,且P到△ABC的三边距离相等,则P是△ABC哪三条线的交点( )
A. 边的垂直平分线B. 角平分线
C. 高线D. 中位线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数y=
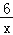 上有两点A(3,2),B(6,1),在直线y=﹣x上有一动点P,当P点的坐标为 时,PA+PB有最小值.
上有两点A(3,2),B(6,1),在直线y=﹣x上有一动点P,当P点的坐标为 时,PA+PB有最小值.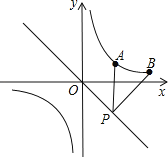
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线
 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线相等的四边形是矩形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. (x+y)2=x2+y2 B. (x﹣y)2=x2﹣2xy﹣y2
C. x(x﹣1)=x2﹣1 D. (x+1)(x﹣1)=x2﹣1
相关试题

