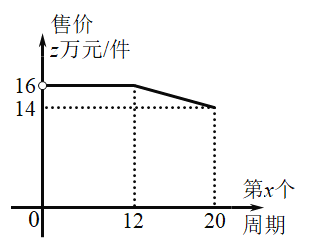
【题目】某工厂计划在每个生产周期内生产并销售完某型设备，设备的生产成本为10万元/件（1）如图，设第x（0＜x≤20）个生产周期设备售价z万元/件，z与x之间的关系用图中的函数图象表示，求z关于x的函数解析式（写出x的范围）．
（2）设第x个生产周期生产并销售的设备为y件，y与x满足关系式y=5x+40（0＜x≤20）．在（1）的条件下，工厂在第几个生产周期创造的利润最大？最大为多少万元？（利润=收入-成本）
【答案】（1）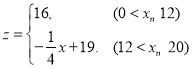
；（2）工厂在第14个生产周期创造的利润最大，最大是605万元．
【解析】
（1）由图像可知，当
，函数为常数函数z=16；当
，函数为一次函数，设函数解析式为
，直线过点(12，16)，(20，14)代入即可求出，从而可得到z关于x的函数解析式；
（2）根据x的不同取值范围，z关于x的关系式不同，设W为利润，当，
，可知x=12时有最大利润；当，
，当
时有最大利润．
解：（1）由图可知，当时，
当时，
是关于
的一次函数，设
则
，得
，即
∴关于的函数解析式为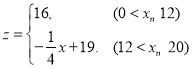
（2）设第个生产周期工厂创造的利润为
万元
①时，
当
时，
（万元）
②时，
当时，
（万元）
综上所述，工厂在第14个生产周期创造的利润最大，最大是605万元．
名校课堂系列答案科目：初中数学 来源： 题型：
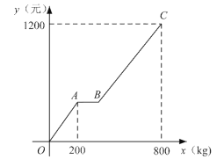
【题目】某商店代理销售一种水果，六月份的销售利润
（元）与销售量
之间函数关系的图像如图中折线所示．请你根据图像及这种水果的相关销售记录提供的信息，解答下列问题：
日期 | 销售记录 |
6月1日 | 库存 |
6月9日 | 从6月1日至今，一共售出 |
6月10、11日 | 这两天以成本价促销，之后售价恢复到10元/ |
6月12日 | 补充进货 |
6月30日 |
|
（1）截止到6月9日，该商店销售这种水果一共获利多少元？
（2）求图像中线段
所在直线对应的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心疾首.今年我校为确保学生安全，开展了“远离溺水珍爱生命”的防溺水安全知识竞赛.现从七、八年级中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组：A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100），下面给出了部分信息：
七年级10名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82 ；
八年级10名学生的竞赛成绩在C组中的数据是：92，90，94.
七、八年级抽取的学生竞赛成绩统计表
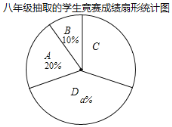
根据以上信息，解答下列问题：
（1）上述图表中a=______，b=______，c=______；
（2） 我校七、八年级共400人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x≥90）的学生人数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，直线
分别交x轴、y轴于A，B两点，经过A，B两点的抛物线
与x轴的正半轴相交于点
．
（1）求抛物线的解析式；
（2）若P为线段AB上一点，
，求AP的长；
（3）在（2）的条件下，设M是y轴上一点，试问：抛物线上是否存在点N，使得以A，P，M，N为顶点的四边形为平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，将函数
为常数)的图象记为
图象
与直线
的交点坐标为
．
（1）若点
在图象上，求
的值；
（2）求
的最小值；
（3）当直线
的图象与函数为常数)的图像只有一个公共点时，求的取值范围；
（4）若
点
在图象上，且点的横坐标为
点关于
轴的对称点为点
.当点不在坐标轴上时，以点
为顶点构造矩形
使点
落在
轴上.当图象与矩形
的边有两个公共点时，直接写出的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，反比例函数
（
）的图象经过点
，过点
的直线
与
轴、
轴分别交于
，
两点．
（1）求反比例函数的表达式；
（2）若
的面积为
的面积的2倍，求此直线的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细，所失弥少，隔之又割，以至不可割，则与圆周合体，而无所失也．”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长．如图1，若用圆的内接正六边形的面积
来近似估计半径为1的⊙O的面积，再用如图2的圆的内接正十二边形的面积
来近似估计半径为1的⊙O的面积，则
____．(结果保留根号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】4月23日是世界读书日，校文学社为了解学生课外阅读的情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：
收集数据：从学校随机抽取20名，进行了每周用于课外阅读时间的调查，数据如下（单位：
）：
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据：按如下分数段整理样本数据并补全表格：
|
|
|
| |
等级 |
|
|
|
|
人数 | 3 |
| 8 | 4 |
分析数据：补全下列表格中的统计量：
平均数 | 中位数 | 众数 |
80 |
|
|
得出结论：
（1）请写出表中
_________；
_________
；
__________；
（2）如果该校现有学生7500人，估计等级为“
”的学生有_________名；
（3）假设平均阅读一本课外书的时间为
，请你选择一种统计量估计该校学生每人一年（按52周计算）平均阅读多少本课外书？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】通过使用手机app购票，智能闸机、手持验票机验票的方式，能够大大缩短游客排队购票、验票的等待时间，且操作极其简单，已知某公园采用新的售票、验票方式后，平均每分钟接待游客的人数是原来的10倍，且接待5000名游客的入园时间比原来接待600名游客的入园时间还少5分钟，求该公园原来平均每分钟接待游客的人数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
