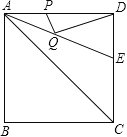
【题目】如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 .
参考答案:
【答案】![]() .
.
【解析】
试题过D作AE的垂线交AE于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
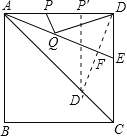
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=2,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=4,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=4,
∴P′D′=![]()
,即DQ+PQ的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0) , 且x1+x2=4,
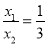 .
.
(1)求抛物线的代数表达式;
(2)设抛物线与y轴交于C点,求直线BC的表达式;
(3)求△ABC的面积.
-
科目: 来源: 题型:
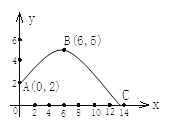
查看答案和解析>>【题目】在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某二次函数图象的一部分(如图),若这个男生出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为B(6,5).
(1)求这个二次函数的表达式;
(2)该男生把铅球推出去多远?(精确到0.01米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段
频数
频率
50.5~60.5
16
0.08
60.5~70.5
40
0.2
70.5~80.5
50
0.25
80.5~90.5
m
0.5
90.5~100.5
24
n

(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y= -x2-2x的图象与x轴交于点A、O,在抛物线上有一点P,满足
S△AOP=3,则点P的坐标是( )
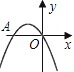
A. (-3,-3) B. (1,-3) C. (-3,-3)或(-3,1) D. (-3,-3)或(1,-3)
-
科目: 来源: 题型:
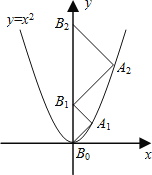
查看答案和解析>>【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=____
相关试题

