【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( )

A.4B.3C.2D.1
参考答案:
【答案】B
【解析】
①利用HL证明可得;
②设AG=x,在△GBE中,利用勾股定理可得到关于x的方程,解得x的值,从而得出GF、GB的值;
③△GDF是直角三角形,直接按照面积公式求解即可;
④先求解出Rt△GBE的面积,△EBF的面积=△GBE的面积×![]() .
.
①∵△EDF是△EDC翻折得到,∴△EDF≌△EDC
∴DF=CD=AD=12,∠EFD=∠ECD=90°=∠GAD
∵GD=GD
∴△FGD≌△AGD,①正确
②设AG=x,则GF=x,GB=12-x
∵BE=EC,∴BE=EC=FE=6
∴在Rt△GBE中,![]() ,即:
,即:![]()
解得:x=4,∴AG=GF=4,BG=8,②正确
③![]() ,③错误
,③错误
④![]()
∴![]() ,④正确
,④正确
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办的”中国汉字听写大会“比赛受到各班的广泛关注,为了了解学生对”中国汉字听写大会“活动的喜爱程度,对部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为A类(非常喜欢),B类(较喜欢),C类(一般),D类(不喜欢).请结合两幅统计图,回答下列问题
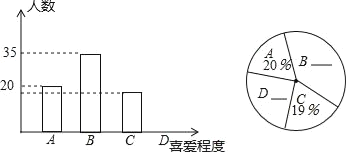
(1)写出本次抽样调查的总人数;
(2)请补全两幅统计图,写出计算过程;
(3)若该校有1500名学生.请你估计对“中国汉字听写大会”此项活动不喜欢的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )

A.①②B.②③C.①③D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售某种玩具,进货价为20元.根据市场调查:在一段时间内,销售单价是30元时,销售量是400件,而销售单价每上涨1元,就会少售出10件玩具,超市要完成不少于300件的销售任务,又要获得最大利润,则销售单价应定为元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利元,商场日销售量件(用含x的代数式表示);
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
相关试题

