【题目】(14分)如图,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.

(1)填空:点C的坐标为( , ),点D的坐标为( , );
(2)设点P的坐标为(a,0),当![]() 最大时,求a的值并在图中标出点P的位置;
最大时,求a的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
参考答案:
【答案】(1)C(0,3),D(1,4);(2)a=﹣3;(3)S= ,当t=
,当t=![]() 时,S有最大值
时,S有最大值![]() .
.
【解析】试题分析:(1)令x=0,得到C的坐标,把抛物线配成顶点式,可得顶点D的坐标;
(2)延长CD交x轴于点P.因为![]() 小于或等于第三边CD,所以当
小于或等于第三边CD,所以当![]() 等于CD时,
等于CD时, ![]() 的值最大.因此求出过CD两点的解析式,求它与x轴交点坐标即可;
的值最大.因此求出过CD两点的解析式,求它与x轴交点坐标即可;
(3)过C点作CE∥x轴,交DB于点E,求出直线BD的解析式,得到点E的坐标,求出P′C′与BC的交点M的坐标,分两种情况讨论:①点C′在线段CE上;②点C′在线段CE的延长线上,再分别求得N点坐标,再利用图形的面积的差,可表示出S,再求得其最大值即可.
试题解析:(1)在![]() 中,令x=0,得到y=3,∴C(0,3),∵
中,令x=0,得到y=3,∴C(0,3),∵![]() =
=![]() ,∴D(1,4),故答案为:C(0,3),D(1,4);
,∴D(1,4),故答案为:C(0,3),D(1,4);
(2)∵在三角形中两边之差小于第三边,∴延长DC交x轴于点P,设直线DC的解析式为![]() ,把D、C两点坐标代入可得:
,把D、C两点坐标代入可得: ![]() ,解得:
,解得: ![]() ,∴直线DC的解析式为
,∴直线DC的解析式为![]() ,将点P的坐标(a,0)代入得a+3=0,求得a=﹣3,如图1,点P(﹣3,0)即为所求;
,将点P的坐标(a,0)代入得a+3=0,求得a=﹣3,如图1,点P(﹣3,0)即为所求;

(3)过点C作CE∥x,交直线BD于点E,如图2,

由(2)得直线DC的解析式为![]() ,易求得直线BD的解析式为
,易求得直线BD的解析式为![]() ,直线BC的解析式为
,直线BC的解析式为![]() ,在
,在![]() 中,当y=3时,x=
中,当y=3时,x=![]() ,∴E点坐标为(
,∴E点坐标为(![]() ,3),设直线P′C′与直线BC交于点M,∵P′C′∥DC,P′C′与y轴交于点(0,3﹣t),∴直线P′C′的解析式为
,3),设直线P′C′与直线BC交于点M,∵P′C′∥DC,P′C′与y轴交于点(0,3﹣t),∴直线P′C′的解析式为![]() ,联立:
,联立: ![]() ,解得:
,解得:  ,∴点M坐标为(
,∴点M坐标为(![]() ,
, ![]() ),∵B′C′∥BC,B′坐标为(3+t,0),∴直线B′C′的解析式为
),∵B′C′∥BC,B′坐标为(3+t,0),∴直线B′C′的解析式为![]() ,
,
分两种情况讨论:①当![]() 时,如图2,B′C′与BD交于点N,联立
时,如图2,B′C′与BD交于点N,联立![]() :,解得:
:,解得: ![]() ,∴N点坐标为(3﹣t,2t),S=S△B′C′P﹣S△BMP﹣S△BNB′=
,∴N点坐标为(3﹣t,2t),S=S△B′C′P﹣S△BMP﹣S△BNB′=![]() ×6×3﹣
×6×3﹣![]() (6﹣t)×
(6﹣t)×![]() (6﹣t)﹣
(6﹣t)﹣![]() t×2t=
t×2t=![]() ,其对称轴为t=
,其对称轴为t=![]() ,可知当
,可知当![]() 时,S随t的增大而增大,当t=
时,S随t的增大而增大,当t=![]() 时,有最大值
时,有最大值![]() ;
;
②当![]() 时,如图3,直线P′C′与DB交于点N,
时,如图3,直线P′C′与DB交于点N,

联立: ![]() ,解得:
,解得:  ,∴N点坐标为(
,∴N点坐标为(![]() ,
, ![]() ),S=S△BNP′﹣S△BMP′=
),S=S△BNP′﹣S△BMP′=![]() (6﹣t)×
(6﹣t)×![]() ﹣
﹣![]() ×(6﹣t)×
×(6﹣t)×![]() =
=![]() =
=![]() ;
;
显然当![]() <t<6时,S随t的增大而减小,当t=
<t<6时,S随t的增大而减小,当t=![]() 时,S=
时,S=![]()
综上所述,S与t之间的关系式为S= ,且当t=
,且当t=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() .
.
∵![]() ,∴当t=
,∴当t=![]() 时,S有最大值
时,S有最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x取时,式子(x﹣10)2+8有最小值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(6,y)在第四象限,则y的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2010年春季我国西南五省持续干旱,旱情牵动着全国人民的心.“一方有难、八方支援”,某厂计划生产1 800吨纯净水支援灾区人民,为尽快把纯净水发往灾区,工人把每天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任务.求原计划每天生产多少吨纯净水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我国
 年税收收入及其增长速度的不完整统计图
年税收收入及其增长速度的不完整统计图 请你根据图中已有信息,解答下列问题:
请你根据图中已有信息,解答下列问题:
 这5年中,哪一年至哪一年的年税收收入增长率持续上升?
这5年中,哪一年至哪一年的年税收收入增长率持续上升? 求出2008年我国的年税收收入
求出2008年我国的年税收收入 精确到1亿元
精确到1亿元
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中的x的值
(1)4x2﹣16=0;
(2)(x﹣2)3=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
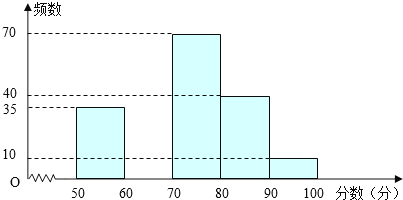
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
相关试题

